题目内容
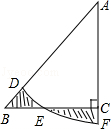
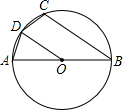
已知：AB为⊙O的直径，半径OD∥弦BC，且AD=1，AB=4，那么cos∠B的值为（ ）
A．
| B．
| C．
| D．
|
连接AC，交OD于E．
∵AB为⊙O的直径，
∴∠ACB=90°，
∵OD∥BC，
∴∠AEO=∠ACB=90°，∠AOE=∠B．
设OE=x，则DE=OD-OE=2-x．
∵AE2=OA2-OE2=AD2-DE2，
∴22-x2=12-（2-x）2，
解得x=
．
在△OAE中，∠AEO=90°，
∴cos∠AOE=
=
=
，
∴cos∠B=cos∠AOE=
．
故选A．
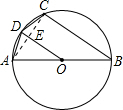
∵AB为⊙O的直径，
∴∠ACB=90°，
∵OD∥BC，
∴∠AEO=∠ACB=90°，∠AOE=∠B．
设OE=x，则DE=OD-OE=2-x．
∵AE2=OA2-OE2=AD2-DE2，
∴22-x2=12-（2-x）2，
解得x=
| 7 |
| 4 |
在△OAE中，∠AEO=90°，
∴cos∠AOE=
| OE |
| OA |
| ||
| 2 |
| 7 |
| 8 |
∴cos∠B=cos∠AOE=
| 7 |
| 8 |
故选A．
练习册系列答案
同步练习强化拓展系列答案
相关题目
的长.
