题目内容
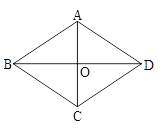
(10分)如图,平行四边形ABCD中,对角线AC,BD交于O点,过O点作直线EF,交AD,BC于E,F,

(1)试说明OE="OF"
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?试说明你的结论

(1)试说明OE="OF"
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?试说明你的结论
解:(1)△AOE≌△COF ∴OE=OF
(2)S =S
=S 。
。
(2)S
 =S
=S 。
。试题分析:(1)∵四边形ABCD是平行四边形, ∴ AO=OC,AD‖BC,
∴∠EAO =∠FCO,在△AOE和△COF中, 又因为对顶角相等

∴ △AOE≌△COF(ASA)
∴OE=OF
(2)∵四边形ABCD是平行四边形,
∴AB="CD,BC=AD," ∠ABC=∠CAD, ,△AOE≌△COF
∴△ABC≌△CDA(全等三角形的面积相等)
又∵△AOE≌△COF,
∴S
 =S
=S ,
,∴S
 =S
=S 这两个四边形面积相等
这两个四边形面积相等点评:难度系数较大,此题考查了平行四边形的性质,全等三角形的判定和性质,利用全等的性质可以得出面积相等。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 cm,则另一条对角线的长( )
cm,则另一条对角线的长( )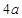 ,CF=
,CF=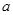 ,则正方形ABCD的面积为 .
,则正方形ABCD的面积为 .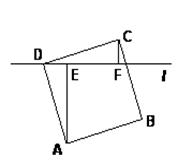



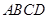 的面积为120,
的面积为120,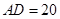 ,
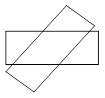
,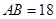 .沿两对角线将四边形
.沿两对角线将四边形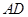 、
、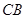 重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 .
重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 .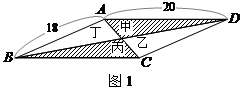
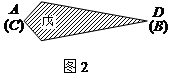

 ,OB=4
,OB=4