题目内容
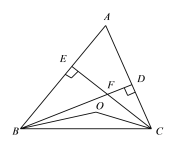
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

求证:△CED是等腰直角三角形
证明:∵∠1=∠2( )
∴EC= (在一个三角形中,等角对等边)
∵∠A=∠B=90°,AE=BC
∴△AED≌△BCE( )
∴∠AED=∠ ( )
∵∠BCE+∠BEC=90°
∠ +∠BEC=90°(等量代换)
∴∠DEC=90°.
∴△CED是等腰直角三角形.
【答案】已知,DE,HL,BCE,全等三角形的性质,AED.
【解析】
根据∠1=∠2,得到EC=DE,证明△AED≌△BCE全等,利用全等性质,找到△CED是等腰直角三角形.
证明:∵∠1=∠2(已知)
∴EC=DE(在一个三角形中,等角对等边)
∵∠A=∠B=90°,AE=BC
∴△AED≌△BCE(HL)
∴∠AED=∠BCE(全等三角形的性质)
∵∠BCE+∠BEC=90°
∠AED+∠BEC=90°(等量代换)
∴∠DEC=90°.
∴△CED是等腰直角三角形.
故答案为:已知,DE,HL,BCE,全等三角形的性质,AED.

练习册系列答案
相关题目