题目内容
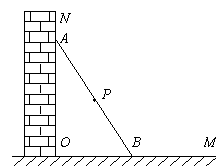
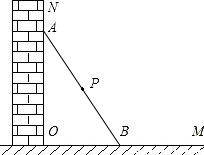
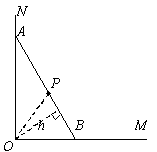
如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P。若木棍A端沿墙下滑,且B端沿地面向右滑行。
(1)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由。
(2)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值。
(1)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由。
(2)在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值。
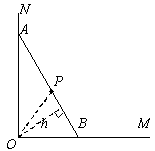
解:(1)不变。理由:在直角三角形中,斜边上的中线等于斜边的一半,因为斜边AB不变,所以斜边上的中线OP不变。
(2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大。
如图,若h与OP不相等,则总有h<OP,
故根据三角形面积公式,有h与OP相等时△AOB的面积最大
此时,S△AOB=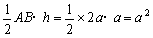 ,所以△AOB的最大面积为
,所以△AOB的最大面积为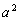 。
。
(2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大。
如图,若h与OP不相等,则总有h<OP,
故根据三角形面积公式,有h与OP相等时△AOB的面积最大
此时,S△AOB=
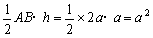 ,所以△AOB的最大面积为
,所以△AOB的最大面积为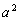 。
。 

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.