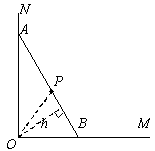题目内容
如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离是否变化?并简述理由.
【答案】分析:根据直角三角形斜边上中线等于斜边的一半得出OP= AB=a,即可得出答案.
AB=a,即可得出答案.
解答: 解:在木棍滑动的过程中,点P到点O的距离不发生变化,理由是:
解:在木棍滑动的过程中,点P到点O的距离不发生变化,理由是:
连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,
∴OP= AB=a,
AB=a,
即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a.
点评:本题考查了直角三角形斜边上中线性质的应用,关键是求出OP长.
 AB=a,即可得出答案.
AB=a,即可得出答案.解答:
 解:在木棍滑动的过程中,点P到点O的距离不发生变化,理由是:
解:在木棍滑动的过程中,点P到点O的距离不发生变化,理由是:连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,
∴OP=
 AB=a,
AB=a,即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a.
点评:本题考查了直角三角形斜边上中线性质的应用,关键是求出OP长.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.