Question

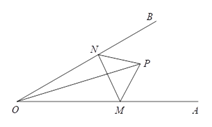
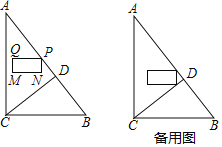
【题目】如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝6．CD⊥AB于点D．点P从点A出发，以每秒1个单位长度的速度沿线段AB向终点B运动．在运动过程中，以点P为顶点作长为2，宽为1的矩形PQMN，其中PQ＝2，PN＝1，点Q在点P的左侧，MN在PQ的下方，且PQ总保持与AC垂直．设P的运动时间为t（秒）（t＞0），矩形PQMN与△ACD的重叠部分图形面积为S（平方单位）．

（1）求线段CD的长；

（2）当矩形PQMN与线段CD有公共点时，求t的取值范围；

（3）当点P在线段AD上运动时，求S与t的函数关系式．

Answer 1

【答案】（1）CD＝；（2）≤t≤；（3）当0＜t＜时，S＝；当≤t≤时，S＝2；当＜t≤时，S=-t2+t-．

【解析】

（1）由勾股定理得出AB＝,由△ABC的面积得出ACBC＝ABCD，即可得出CD的长；

（2）分两种情形：①当点N在线段CD上时，如图1所示，利用相似三角形的性质求解即可．②当点Q在线段CD上时，如图2所示，利用相似三角形的性质求解即可．

（3）首先求出点Q落在AC上的运动时间t，再分三种情形：①当0＜t＜时，重叠部分是矩形PHYN，如图4所示，②当≤t≤时，重合部分是矩形PQMN，S＝PQPN＝2．③当＜t≤时，如图5中重叠部分是五边形PQMJI，分别求解即可．

（1）∵∠ACB＝90°，AC＝8，BC＝6，

∴AB＝，

∵S△ABC＝ACBC＝ABCD，

∴ACBC＝ABCD，即：8×610×CD，

∴CD＝；

（2）在Rt△ADC中，AD＝，BD＝AB－AD＝10－＝，

当点N在线段CD上时，如图1所示：

∵矩形PQMN，PQ总保持与AC垂直，

∴PN∥AC，

∴∠NPD＝∠CAD，

∵∠PDN＝∠ADC，

∴△PDN∽△ADC，

∴，即：，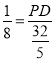

解得：PD＝，

∴t＝AD－PD＝，

当点Q在线段CD上时，如图2所示：

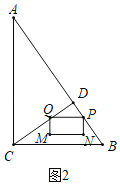
∵PQ总保持与AC垂直，

∴PQ∥BC，△DPQ∽△DBC，

∴，即：，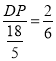

解得：DP＝ ，

∴t＝AD+DP＝，

∴当矩形PQMN与线段CD有公共点时，t的取值范围为≤t≤；

（3）当Q在AC上时，如图3所示：

∵PQ总保持与AC垂直，

∴PQ∥BC，△APQ∽△ABC，

∴，即：，

解得：AP＝ ，

当0＜t＜时，重叠部分是矩形PHYN，如图4所示：

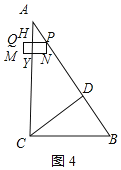
∵PQ∥BC，

∴△APH∽△ABC，

∴，即：，

∴PH＝，

∴S＝PHPN＝；

当≤t≤时，重合部分是矩形PQMN，S＝PQPN＝2．

当＜t≤时，如图5中重叠部分是五边形PQMJI，

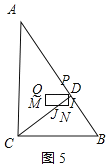
S＝S矩形PNMQ-S△JIN＝2- （t-）[1-（-t）]＝-t2+t-．