Question

【题目】如图所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=________.

Answer 1

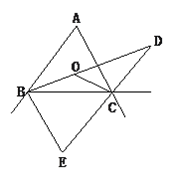
【答案】 120° 30° 60°

【解析】∵BO平分∠ABC，CO平分∠ACB，
∴∠ABC=2∠1，∠ACB=2∠2，
又∵∠ABC+∠ACB+∠A=180°，
∴2∠2+2∠1+∠A=180°，
∴∠2+∠1=90°-∠A，
又∵∠2+∠1+∠BOC=180°，
∴90°-∠A+∠BOC=180°，
∴∠BOC=90°+∠A，
而∠A=50°，
∴∠BOC=90°+×60°=120°，
∵∠DCF=∠D+∠DBC，∠ACF=∠ABC+∠A，BD平分∠ABC，DC平分∠ACF，
∴∠ACF=2∠DCF，∠ABC=2∠DBC，
∴2∠D+2∠DBC=∠ABC+∠A，
∴2∠D=∠A，即∠D=∠A．
∵∠A=60°，
∴∠D=30°，
∵BE平分∠ABC相邻外角，BD平分∠ABC，
∴∠DBE=90°，
∴∠E=90°-∠D=60°，
故答案是：120°，30°60°．