题目内容
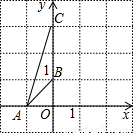
(2009•黄埔区一模)已知二次函数图象的顶点为(-2,5),图象与y轴交点A的坐标为(0,3).(1)求该函数的解析式;
(2)求该二次函数图象与x轴交点B、C的坐标.
【答案】分析:①已知顶点,一般应该设抛物线解析式的顶点式,只需要求待定系数a的值即可确定解析式;
②求图象与x轴的交点,令y=0,解一元二次方程,求两根即可.
解答:解:(1)设这个二次函数的解析式为y=a(x-h)2+k
依题意得
解得
所求二次函数的解析式为y=- (x+2)2+5
(x+2)2+5
(2)令y=0,解方程- (x+2)2+5=0
(x+2)2+5=0
得x1=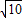 -2,x2=-
-2,x2=- -2
-2
所以该二次函数图象与x轴的两个交点B、C的坐标为( ,0)、(
,0)、( ,0).
,0).
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组与一元二次方程的解法等知识,难度不大.
②求图象与x轴的交点,令y=0,解一元二次方程,求两根即可.
解答:解:(1)设这个二次函数的解析式为y=a(x-h)2+k
依题意得

解得

所求二次函数的解析式为y=-
 (x+2)2+5
(x+2)2+5(2)令y=0,解方程-
 (x+2)2+5=0
(x+2)2+5=0得x1=
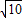 -2,x2=-
-2,x2=- -2
-2所以该二次函数图象与x轴的两个交点B、C的坐标为(
 ,0)、(
,0)、( ,0).
,0).点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组与一元二次方程的解法等知识,难度不大.

练习册系列答案
相关题目
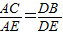 .
.