题目内容
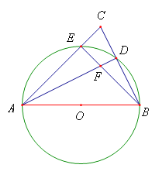
【题目】已知在圆O中，AB是直径，点E和点D是圆O上的点，且∠EAB=45°，延长AE和BD相交于点C，连接BE和AD交于点F，BD=12，CD=8，则直径AB的长是_____．
【答案】
【解析】
连接ED，设
，
，先证的
是等腰直角三角形，再根据勾股定理得出
，据此列出方程；再根据圆内接四边形的性质得出
，然后证得
，最后根据相似的性质得出
，据此列出方程，解方程得出
的值，再根据是等腰直角三角形即可求得直径
的长.
连接ED，如选图所示
设，，
∵是直径，
∴
∴
∴是等腰直角三角形
∴
∵
∴
∴
∴
∵四边形
是圆
的内接四边形
∴
∴
∴，即
∴
，则
∴把①代入②中得：
解得：
或
∵只有当
与圆相切时
才是等腰直角三角形，
才等于
∴本题中显然
∴
∴（舍去）
又∵
都表示线段长度
∴
∴
故填：.
练习册系列答案
相关题目
