题目内容
如图,已知直线 过点
过点 和
和 ,
, 是
是 轴正半轴上的动点,
轴正半轴上的动点, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 轴于点
轴于点 .
.
(1)直接写出直线 的解析式;
的解析式;
(2)当 时,设
时,设 ,
, 的面积为
的面积为 ,求S关于t的函数关系式;并求出S的最大值;
,求S关于t的函数关系式;并求出S的最大值;
(3)当点Q在线段AB上(Q与A、B不重合)时,直线 过点A且与x轴平行,问在
过点A且与x轴平行,问在 上是否存在点C,使得
上是否存在点C,使得 是以
是以 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
(1)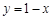 ;
;
(2)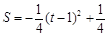 ,当
,当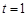 时,S有最大值
时,S有最大值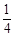 ;
;
(3)在 上存在点
上存在点 ,使得
,使得 是以
是以 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
解析试题分析:(1)已知直线L过A,B两点,可将两点的坐标代入直线的解析式中,用待定系数法求出直线L的解析式;
(2)求三角形OPQ的面积,就需知道底边OP和高QM的长,已知了OP为t,关键是求出QM的长.已知了QM垂直平分OP,那么OM= ,
, ,再求即可;
,再求即可;
(3)如果存在这样的点C,那么CQ=QP=OQ,因此C,O就关于直线BL对称,因此C的坐标应该是(1,1).那么只需证明CQ⊥PQ即可.分情况进行讨论.
试题解析:(1)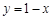 ;
;
(2)∵ ,∴Q点的横坐标为
,∴Q点的横坐标为 ,
,
当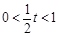 ,即
,即 时,
时, ,
,
∴ .
.
当 时,
时, ,
,
∴当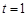 时,S有最大值
时,S有最大值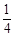 ;
;
(3)∵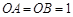 ,∴
,∴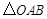 是等腰直角三角形,
是等腰直角三角形,
若在 上存在点
上存在点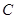 ,使得
,使得 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则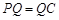 ,
,
∴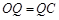 ,∵
,∵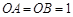 、
、 轴,∴
轴,∴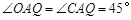
O、C关于直线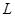 对称∴
对称∴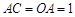 ,得
,得 .
.
连接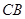 ,则四边形
,则四边形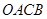 是正方形.
是正方形.
(i)当点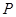 在线段
在线段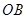 上,如图–1.
上,如图–1.
由对称性,得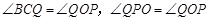 ,
,
∴ ,
,
∴ .
.
即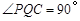
(ii)当点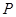 在线段
在线段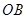 的延长线上,如图–2,
的延长线上,如图–2,
∵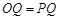 ∴
∴ 由对称性可知
由对称性可知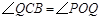
∴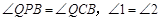 ,
,
∴ .
.
综合(i)(ii),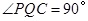 .
.
∴在 上存在点
上存在点 ,使得
,使得 是以
是以 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
考点:二次函数综合题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 x+c与x轴交于点A(4,0)、B(-1,0),与y轴交于点C,连接AC,点M是线段OA上的一个动点(不与点O、A重合),过点M作MN∥AC,交OC于点N,将△OMN沿直线MN折叠,点O的对应点O′落在第一象限内,设OM=t,△O′MN与梯形AMNC重合部分面积为S.
x+c与x轴交于点A(4,0)、B(-1,0),与y轴交于点C,连接AC,点M是线段OA上的一个动点(不与点O、A重合),过点M作MN∥AC,交OC于点N,将△OMN沿直线MN折叠,点O的对应点O′落在第一象限内,设OM=t,△O′MN与梯形AMNC重合部分面积为S.
 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
 ),M是OA的中点.
),M是OA的中点.

 ,顶点随着t的增大向上移动时,求t的取值范围.
,顶点随着t的增大向上移动时,求t的取值范围.
 (
( 为常数,且
为常数,且 )与
)与 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线 与抛物线的另一交点为D.
与抛物线的另一交点为D.
 交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法: 时,BP2=BO•BA;
时,BP2=BO•BA; .
.