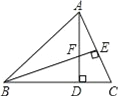
ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдкжБНЧзјБъЯЕxoyжаЃЌOЪЧзјБъдЕуЃЌЕуAдкxе§АыжсЩЯЃЌOAЃН![]() cmЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌOBЃН12cmЃЌЖЏЕуPДгЕуOПЊЪМбиOAвд
cmЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌOBЃН12cmЃЌЖЏЕуPДгЕуOПЊЪМбиOAвд![]() cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBOвд2cm/sЕФЫйЖШЯђЕуOвЦЖЏ.ШчЙћPЁЂQЁЂRЗжБ№ДгOЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉs.
cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBOвд2cm/sЕФЫйЖШЯђЕуOвЦЖЏ.ШчЙћPЁЂQЁЂRЗжБ№ДгOЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉs.
ЃЈ1ЃЉЧѓЁЯOABЕФЖШЪ§.
ЃЈ2ЃЉвдOBЮЊжБОЖЕФЁбOЁфгыABНЛгкЕуMЃЌЕБtЮЊКЮжЕЪБЃЌPMгыЁбOЁфЯрЧаЃП
ЃЈ3ЃЉЪЧЗёДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіГіЕФtжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1) 30ЁуЃЎ(2) t=3ЪБЃЌPMгыЁбOЁЏЯрЧаЃЎ(3) t=8-2![]() ЃЌ
ЃЌ ![]() ЃЌ1+
ЃЌ1+![]() ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉдкRtЁїOABжаЃЌвбжЊСЫOAЁЂOBЕФГЄЃЌМДПЩЧѓГіЁЯOABЕФе§ЧажЕЃЌгЩДЫПЩЕУЕНЁЯOABЕФЖШЪ§ЃЛ
ЃЈ2ЃЉСЌНгOЁфMЃЌЕБPMгыЁбOЁфЯрЧаЪБЃЌPMЁЂPOЭЌЮЊЁбOЁфЕФЧаЯпЃЌвзжЄЕУЁїOOЁфPЁеЁїMOЁфPЃЌдђЁЯOOЁфP=ЁЯMOЁфPЃЛдкЃЈ1ЃЉжавзЕУЁЯOBA=60ЁуЃЌМДЁїOЁфBMЪЧЕШБпШ§НЧаЮЃЌгЩДЫПЩЕУЕНЁЯBOЁфM=ЁЯPOЁфM=ЁЯPOЁфO=60ЁуЃЛдкRtЁїOPOЁфжаЃЌИљОнЁЯPOЁфOЕФЖШЪ§МАOOЁфЕФГЄМДПЩЧѓЕУOPЕФГЄЃЌвбжЊСЫPЕуЕФдЫЖЏЫйЖШЃЌМДПЩИљОнЪБМф=ТЗГЬЁТЫйЖШЧѓЕУtЕФжЕЃЛ
ЃЈ3ЃЉДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃЌгЩгкЁїQPQЕФбќКЭЕзВЛШЗЖЈЃЌашЗжРрЬжТлЃКЂйPR=RQЃЌЂкPR=PQЃЌЂлRQ=PQЪБЗжБ№ЧѓГіЗћКЯЬтвтЕФtжЕМДПЩЃЌ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкRtЁїAOBжаЃК
tanЁЯOAB=![]() ЃЌ
ЃЌ
ЁрЁЯOAB=30ЁуЃЎ
ЃЈ2ЃЉШчЭМЃЌСЌНгOЁфPЃЌOЁфMЃЎ
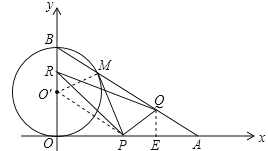
ЕБPMгыЁбOЁфЯрЧаЪБЃЌгаЃК
ЁЯPMOЁф=ЁЯPOOЁф=90ЁуЃЌ
ЁїPMOЁфЁеЁїPOOЁфЃЎ
гЩЃЈ1ЃЉжЊЁЯOBA=60ЁуЃЌ
ЁпOЁфM=OЁфBЃЌ
ЁрЁїOЁфBMЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBOЁфM=60ЁуЃЎ
ПЩЕУЁЯOOЁфP=ЁЯMOЁфP=60ЁуЃЎ
ЁрOP=OOЁфtanЁЯOOЁфP
=6ЁСtan60Ёу=6![]() ЃЌ
ЃЌ
гжЁпOP=2![]() tЃЌ
tЃЌ
Ёр2![]() t=6
t=6![]() ЃЌ
ЃЌ
t=3ЃЎ
МДЃКt=3ЪБЃЌPMгыЁбOЁЏЯрЧаЃЎ
ЃЈ3ЃЉДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃЌ
РэгЩШчЯТЃКгЩЬтвтПЩжЊЃКPR2=16t2-48tЃЌPQ2=52t2-288tЃЌRQ2=28t2-240t+576ЃЌ
ЕБЂйPR=RQЪБЃЌПЩЕУt=8-2![]() ЃЈt=8+
ЃЈt=8+![]() ЩсШЅЃЉЃЛ
ЩсШЅЃЉЃЛ
ЕБЂкPR=PQЪБЃЌПЩЕУt=![]() ЃЛ
ЃЛ
ЕБЂлRQ=PQЪБЃЌПЩЕУt=1+![]() ЃЈt=1-
ЃЈt=1-![]() ЩсШЅЃЉ
ЩсШЅЃЉ
злЩЯПЩжЊЃКЕБt=8-2![]() ЃЌ
ЃЌ ![]() ЃЌ1+
ЃЌ1+![]() ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ