题目内容
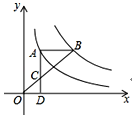
【题目】已知直线y=kx+b经过点B(1,4),且与直线y=-x-11平行.
(1)求直线AB的解析式并求出点C的坐标;
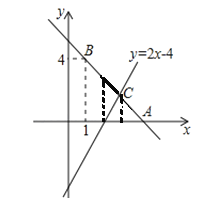
(2)根据图象,写出关于x的不等式0<2x﹣4<kx+b的解集;
(3)现有一点P在直线AB上,过点P做PQ∥y轴交直线y=2x-4于点Q,若C点到线段PQ的距离为1,求点P的坐标并直接写出线段PQ的长.

【答案】(1)y=-x+5,C(3,2); (2)2<x<3 ; (3)P(2,3)或者(4,1),线段PQ的长为3.
【解析】试题分析:(1)待定系数法列方程组求一次函数解析式,联立方程组求两个一次函数的交点.
(2)由一次函数与不等式的关系可知.
(3) 根据C点到线段PQ的距离为1,代入直线解析式求得P点坐标,再求Q点坐标.
试题解析:
解:(1)∵直线y=kx+b经过点B(1,4),函数与直线y=-x-11,
∴![]() ,
,
解得, ![]() ,
,
∴直线AB的解析式为:y=﹣x+5;
∵若直线y=2x﹣4与直线AB相交于点C,
∴![]()
解得![]() ,
,
∴点C(3,2).
(2)由题意知所求是如图位置, ![]() ,令y=0,x=2,C(3,2),
,令y=0,x=2,C(3,2),
所以图像中的部分对应的2<x<3.
(3) 若C点到线段PQ的距离为1,所以P点横坐标是2,或者4,代入直线解析式y=﹣x+5有P(2,3)或者(4,1),代入![]() ,Q(2,0),(4,4),所以PQ=3.
,Q(2,0),(4,4),所以PQ=3.
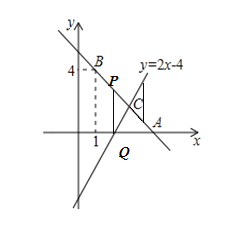

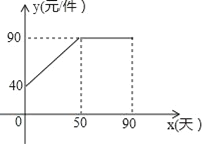
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.