题目内容
如图,在梯形 中,
中, ,
, ,
, ,
, 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形 的高.
的高.
(1)求证:四边形AEFD是平行四边形;
(2)设 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.

 中,
中, ,
, ,
, ,
, 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形 的高.
的高.(1)求证:四边形AEFD是平行四边形;
(2)设
 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.
(1) 证明: ∵ ,∴梯形ABCD为等腰梯形.
,∴梯形ABCD为等腰梯形.
∵∠C=60°,∴ .
.
又∵ ,∴
,∴ .
.
∴ .∴
.∴ .
.
由已知 ,∴AE∥DC.
,∴AE∥DC.
又∵AE为等腰三角形ABD的高, ∴E是BD的中点,
∵F是DC的中点, ∴EF∥BC. ∴EF∥AD.
∴四边形AEFD是平行四边形.
(2)解:在Rt△AED中,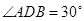 ,∵
,∵ ,∴
,∴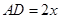 .
.
在Rt△DGC中 ∠C=60°,并且 ,∴
,∴ .
.
由(1)知: 在平行四边形AEFD中 ,又∵
,又∵ ,∴
,∴ ,
,
∴四边形DEGF的面积 ,
,
∴
 .
.
 ,∴梯形ABCD为等腰梯形.
,∴梯形ABCD为等腰梯形.∵∠C=60°,∴
 .
.又∵
 ,∴
,∴ .
.∴
 .∴
.∴ .
.由已知
 ,∴AE∥DC.
,∴AE∥DC. 又∵AE为等腰三角形ABD的高, ∴E是BD的中点,
∵F是DC的中点, ∴EF∥BC. ∴EF∥AD.
∴四边形AEFD是平行四边形.
(2)解:在Rt△AED中,
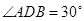 ,∵
,∵ ,∴
,∴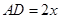 .
.在Rt△DGC中 ∠C=60°,并且
 ,∴
,∴ .
.由(1)知: 在平行四边形AEFD中
 ,又∵
,又∵ ,∴
,∴ ,
,∴四边形DEGF的面积
 ,
,∴

 .
. (1) 综合利用等腰梯形性质以及等腰三角形的性质解决;(2)因为所求四边形的对角线互相垂直,所以其面积可以用对角线乘积的一半表示.

练习册系列答案
相关题目
 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点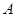 在
在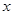 轴上,点
轴上,点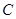 在
在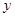 轴上,将边
轴上,将边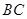 折叠,使点
折叠,使点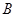 落在边
落在边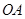 的点
的点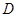 处.已知折叠
处.已知折叠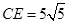 ,且
,且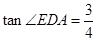 .
.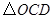 与
与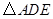 是否相似?请说明理由;
是否相似?请说明理由; 与
与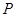 的坐标;
的坐标;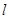 ,使直线
,使直线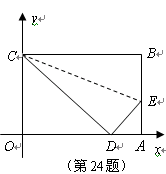


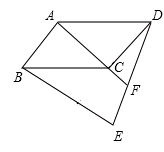

 中,
中, 、
、 分别为
分别为 、
、 边上的点,要使
边上的点,要使 需添加一个条件: .
需添加一个条件: .
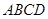 ,有以下四个条件:①
,有以下四个条件:①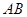 ∥
∥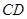 ;②
;②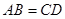 ;③
;③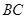 ∥
∥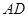 ;④
;④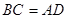 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形