题目内容
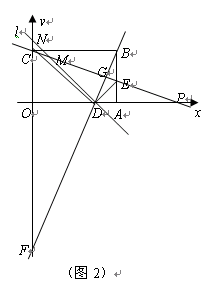
如图,四边形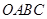 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点 在
在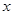 轴上,点
轴上,点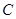 在
在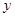 轴上,将边
轴上,将边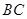 折叠,使点
折叠,使点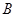 落在边
落在边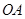 的点
的点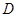 处.已知折叠
处.已知折叠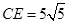 ,且
,且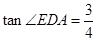 .
.
(1)判断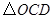 与
与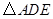 是否相似?请说明理由;
是否相似?请说明理由;
(2)求直线 与
与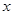 轴交点
轴交点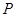 的坐标;
的坐标;
(3)是否存在过点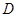 的直线
的直线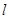 ,使直线
,使直线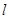 、直线
、直线 与
与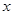 轴所围成的三角形和直线
轴所围成的三角形和直线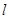 、直线
、直线 与
与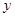 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.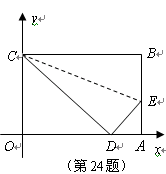
 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点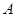 在
在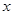 轴上,点
轴上,点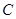 在
在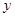 轴上,将边
轴上,将边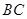 折叠,使点
折叠,使点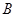 落在边
落在边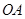 的点
的点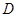 处.已知折叠
处.已知折叠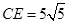 ,且
,且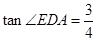 .
.(1)判断
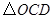 与
与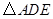 是否相似?请说明理由;
是否相似?请说明理由;(2)求直线
 与
与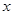 轴交点
轴交点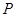 的坐标;
的坐标;(3)是否存在过点
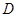 的直线
的直线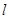 ,使直线
,使直线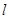 、直线
、直线 与
与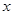 轴所围成的三角形和直线
轴所围成的三角形和直线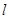 、直线
、直线 与
与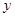 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
解:(1)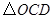 与
与 相似.
相似.
理由如下:
由折叠知, ,
,
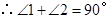 ,
,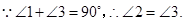
又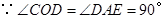 ,
,
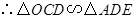 .
.
(2)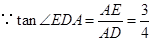 ,
, 设
设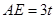 ,
,
则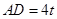 .
.
由勾股定理得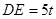 .
.
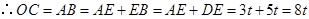 .
.
由(1)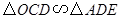 ,得
,得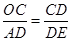 ,
,
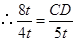 ,
,
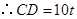 .
.
在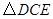 中,
中,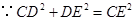 ,
,
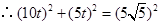 ,解得
,解得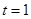 .
.
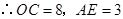 ,点
,点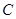 的坐标为
的坐标为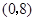 ,
,
点 的坐标为
的坐标为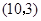 ,
,
设直线 的解析式为
的解析式为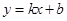 ,
,
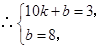 解得
解得
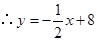 ,则点
,则点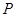 的坐标为
的坐标为 .
.
(3)满足条件的直线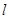 有2条:
有2条: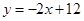 ,
,
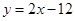 .
.
如图2:准确画出两条直线.
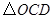 与
与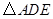 相似.
相似.理由如下:

由折叠知,
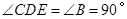 ,
,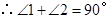 ,
,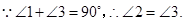
又
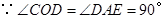 ,
,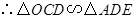 .
.(2)
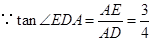 ,
, 设
设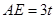 ,
,则
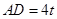 .
.由勾股定理得
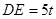 .
.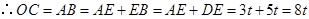 .
.由(1)
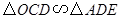 ,得
,得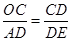 ,
,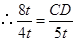 ,
,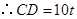 .
.在
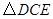 中,
中,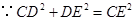 ,
,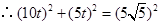 ,解得
,解得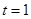 .
.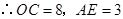 ,点
,点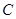 的坐标为
的坐标为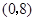 ,
,点
 的坐标为
的坐标为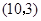 ,
,设直线
 的解析式为
的解析式为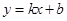 ,
,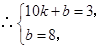 解得
解得
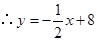 ,则点
,则点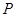 的坐标为
的坐标为 .
.(3)满足条件的直线
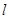 有2条:
有2条: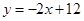 ,
,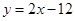 .
.如图2:准确画出两条直线.

(1)由折叠知,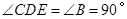 ,根据同角的余角相等可得
,根据同角的余角相等可得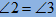 ,再有
,再有
 即可得到
即可得到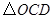 与
与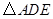 相似;
相似;
(2))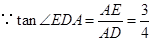 ,
, 设
设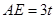 ,则
,则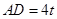 ,由勾股定理得
,由勾股定理得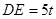 ,
,
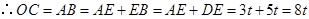 ,由(1)
,由(1)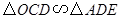 ,根据对应边成比例可得
,根据对应边成比例可得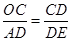 ,
,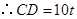 ,在
,在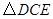 中根据勾股定义即可求出
中根据勾股定义即可求出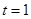 ,从而得到点
,从而得到点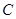 、点
、点 的坐标,再根据待定系数法即可得到直线
的坐标,再根据待定系数法即可得到直线 的解析式,从而得到点
的解析式,从而得到点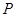 的坐标。
的坐标。
(3)存在,应该有两条如图:
①直线BF,根据折叠的性质可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出两三角形相似,那么可根据B、D两点的坐标求出此直线的解析式.
②直线DN,由于∠FCO=∠NDO,那么可根据∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的长求出ON的值,即可求出N点的坐标,然后根据N、D两点的坐标求出直线DN的解析式.
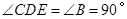 ,根据同角的余角相等可得
,根据同角的余角相等可得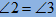 ,再有
,再有 即可得到
即可得到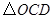 与
与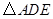 相似;
相似;(2))
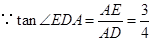 ,
, 设
设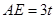 ,则
,则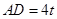 ,由勾股定理得
,由勾股定理得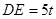 ,
,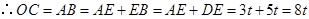 ,由(1)
,由(1)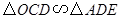 ,根据对应边成比例可得
,根据对应边成比例可得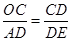 ,
,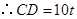 ,在
,在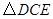 中根据勾股定义即可求出
中根据勾股定义即可求出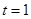 ,从而得到点
,从而得到点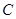 、点
、点 的坐标,再根据待定系数法即可得到直线
的坐标,再根据待定系数法即可得到直线 的解析式,从而得到点
的解析式,从而得到点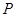 的坐标。
的坐标。(3)存在,应该有两条如图:
①直线BF,根据折叠的性质可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出两三角形相似,那么可根据B、D两点的坐标求出此直线的解析式.
②直线DN,由于∠FCO=∠NDO,那么可根据∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的长求出ON的值,即可求出N点的坐标,然后根据N、D两点的坐标求出直线DN的解析式.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
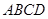 中,
中,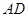 ∥
∥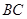 ,
,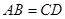 ,
,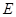 为
为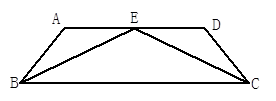
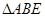 ≌
≌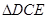 .(2)若
.(2)若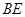 平分
平分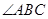 ,且
,且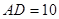 ,求
,求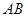 的长.
的长. ,
, ,
, ,
, ,点
,点 在
在 上,
上, ,
, 是
是 中点,在
中点,在 上找一点
上找一点 使
使 的值最小,此时其最小值一定等于( )
的值最小,此时其最小值一定等于( )

 中,
中, ,
, ,
, ,
, 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.
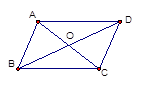
 ABCD中,AC与BD交于点O,点E是BC边的中点,OE=1,则AB的长是 .
ABCD中,AC与BD交于点O,点E是BC边的中点,OE=1,则AB的长是 .
 的边长为6,菱形
的边长为6,菱形 的三个顶点
的三个顶点 分别在正方形
分别在正方形 上,
上, ,连接
,连接 .
. 时,求
时,求 的面积;
的面积; ,用含
,用含 的代数式表示
的代数式表示 ,并说明理由.
,并说明理由.
 ,
,