题目内容
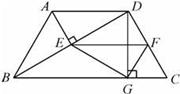
如图,矩形AOBC中,点A的坐标为(0,8),点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为 ( )


| A.30 | B.32 | C.34 | D.16 |
A
解:由折叠可知△ADE和△ACD关于AD成轴对称,
故AE=AC,CD=DE=CB-CD=8-3=5.
所以BE=4,
设OE= ,则OB=AC=AE=x+4.
,则OB=AC=AE=x+4.
在Rt△AOE中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故OB=10.
所以阴影部分的面积为:10×8-2S△ADE=80-50=30(cm2).
故AE=AC,CD=DE=CB-CD=8-3=5.
所以BE=4,
设OE=
 ,则OB=AC=AE=x+4.
,则OB=AC=AE=x+4.在Rt△AOE中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故OB=10.
所以阴影部分的面积为:10×8-2S△ADE=80-50=30(cm2).

练习册系列答案
相关题目
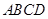 ,
, ,
,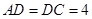 ,
,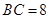 ,点
,点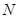 在
在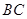 上,
上,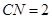 ,
,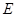 是
是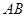 中点,在
中点,在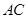 上找一点
上找一点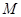 使
使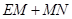 的值最小,此时其最小值一定等于( )
的值最小,此时其最小值一定等于( )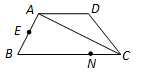
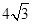
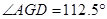 ;②
;②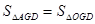 ;③四边形AEFG是菱形;④BE=2OG。
;③四边形AEFG是菱形;④BE=2OG。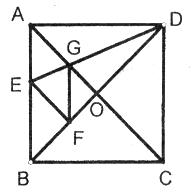
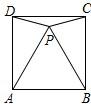
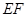 将平行四边形ABCD剪开,则得到的四边形
将平行四边形ABCD剪开,则得到的四边形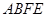 是( )
是( )
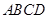 中,
中,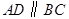 ,
,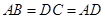 ,
,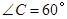 ,
,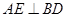 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形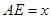 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.