Question

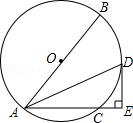
【题目】如图，正方形ABCD的面积为36cm2 ， 点E在BC上，点G在AB的延长线上，四边形EFGB是正方形，以点B为圆心，BC的长为半径画 ，连接AF，CF，则图中阴影部分的面积为 ．

Answer 1

【答案】9πcm2
【解析】解：∵四边形ABCD和四边形EFGB是正方形，且正方形ABCD的面积为36cm2 ， ∴∠G=∠ABC=∠CEF=90°，AB=BC=6，EF=BE=GF=BG，
设EF=BE=GF=BG=a，
则阴影部分的面积S=S扇形BAC+S正方形EFGB+S△CEF﹣S△AGF
= +a2+ a（6﹣a）﹣ （6+a）a
=9π，
故答案为9πcm2 ．
根据正方形的性质得出∠G=∠ABC=∠CEF=90°，AB=BC=6，EF=BE=GF=BG，设EF=BE=GF=BG=a，则阴影部分的面积S=S扇形BAC+S正方形EFGB+S△CEF﹣S△AGF ， 代入求出即可．