题目内容
【题目】阅读下列材料:
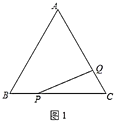
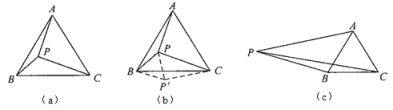
问题:如图(a)所示,已知点![]() 为等边
为等边![]() 内一点,且
内一点,且![]() ,试探究线段
,试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
明明同学的想法是:问题中的线段比较分散,可以通过旋转变换将分散的线段集中在一起,从而解决问题.于是他将![]() 绕点
绕点![]() 顺时针旋转60°,得到了
顺时针旋转60°,得到了![]() ,然后连接
,然后连接![]() .
.
请你参考明明同学的思路,解决下列问题:
(1)图(b)中的![]() 、
、![]() 、
、![]() 之间的数量关系为______.
之间的数量关系为______.
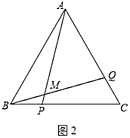
(2)如图(c)所示,点![]() 在等边
在等边![]() 的外部(在直线
的外部(在直线![]() 左侧),满足
左侧),满足![]() ,(1)中的结论仍成立吗?说明你的理由.
,(1)中的结论仍成立吗?说明你的理由.
【答案】(1)![]() ;(2)成立,
;(2)成立,![]() .理由见解析.
.理由见解析.
【解析】
(1)由旋转性质、等边三角形的判定![]() 是等边三角形,由等边三角形的性质知
是等边三角形,由等边三角形的性质知![]() ,求得
,求得![]() ,根据勾股定理可得答案;
,根据勾股定理可得答案;
(2)将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() ,得到了
,得到了![]() ,然后连接
,然后连接![]() ,由旋转性质、等边三角形的判定
,由旋转性质、等边三角形的判定![]() 是等边三角形,求得
是等边三角形,求得![]() ,根据勾股定理可得答案.
,根据勾股定理可得答案.
(1)![]() ;
;
理由是: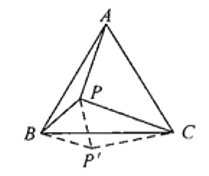
根据旋转的性质得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)成立,即![]() .
.
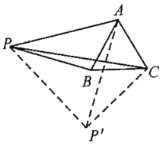
将![]() 绕点A逆时针旋转60°,得到了
绕点A逆时针旋转60°,得到了![]() ,然后连接
,然后连接![]() ,如图所示,
,如图所示,
根据旋转的性质得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
相关题目