Question

【题目】如图，点O是等边△ABC内一点，∠AOB=110，∠BOC=,将△BOC绕点C按顺时针方向旋转60得△ADC，连接OD

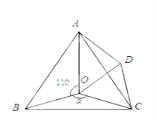
（1）△COD是什么三角形？说明理由；

（2）若AO=，AD=,OD=（为大于1的整数），求的度数

（3）当为多少度时，△AOD是等腰三角形？

Answer 1

【答案】（1））△COD是等边三角形,理由见解析；（2）150；（3）当α的度数为125°或110°或140°时，△AOD是等腰三角形．

【解析】

试题分析：（1）根据旋转的性质可得OC=DC，又∠ODC=60，即可判断△COD是等边三角形；（2）由可判断△ADO是直角三角形，所以∠=∠ADC=90+60=150；（3）分AD=DO，AO=OD，AD=AO三种情况讨论即可．

试题解析：（1）△COD是等边三角形,

理由：由旋转性质得OC=DC ，又∠OCD=60

∴△COD是等边三角形；

（2）当AO=，AD=,OD=时，

有

∴△ADO是直角三角形

所以∠=∠ADC=90+60=150；

解：①要使AO=AD，需∠AOD=∠ADO，

∵∠AOD=360°-110°-60°-α=190°-α，∠ADO=α-60°，

∴190°-α=α-60°，

∴α=125°；

②要使OA=OD，需∠OAD=∠ADO．

∵∠OAD=180°-（∠AOD+∠ADO）=180°-（190°-α+α-60°）=50°，

∴α-60°=50°，

∴α=110°；

③要使OD=AD，需∠OAD=∠AOD．

∵∠OAD=360°-110°-60°-α=190°-α，

∠AOD==120°-，

∴190°-α=120°-，

解得α=140°．

综上所述：当α的度数为125°或110°或140°时，△AOD是等腰三角形．