题目内容
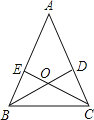
【题目】如图,以△ABC的三边AB、BC、CA分别为边,在BC的同侧作等边△ABD、等边△BCE、等边△CAE,求证:四边形ADEF是平行四边形.

【答案】证明见解析
【解析】分析:由△ABD,△EBC都是等边三角形,易证得△DBE≌△ABC(SAS),则可得DE=AC,又由△ACF是等边三角形,即可得DE=AF,同理可证得AD=EF,即可判定四边形ADEF是平行四边形.
本题解析:
证明:∵△ABD,△EBC都是等边三角形,
∴AD=BD=AB,BC=BE=EC,
∠DBA=∠EBC=60°,
∴∠DBE+∠EBA=∠ABC+∠EBA,
∴∠DBE=∠ABC,
在△DBE和△ABC中,∵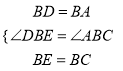 ,
,
∴△DBE≌△ABC(SAS),
∴DE=AC,
又∵△ACF是等边三角形,
∴AC=AF,
∴DE=AF,
同理可证:AD=EF,
∴四边形ADEF是平行四边形.

练习册系列答案
相关题目