题目内容
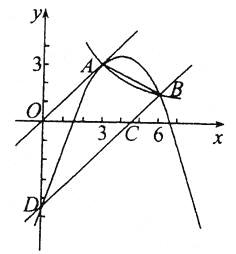
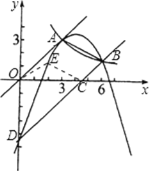
【题目】如图,正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点.
(1)求 m的值;
( 2 )求过 A、B、D 三点的抛物线的解析式;
( 3 )若点E是抛物线上的一个动点,是否存在点 E,使四边形 OECD 的面积S1,是四边形OACD 面积S的![]() ?若存在,求点 E 的坐标;若不存在,请说明理由.
?若存在,求点 E 的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)抛物线的解析式为
;(2)抛物线的解析式为![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)由于反比例函数的图象都经过点A(3,3),由此可以确定函数的解析式,又把直线OA向下平移后,与反比例函数的图象交于点B(6,m),把B的坐标代入反比例函数的解析式即可确定m的值;
(2)由于直线OA向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点,由此首先确定直线BD的解析式,接着可以确定C,D的坐标,最后利用待定系数法即可确定过A、B、D三点的抛物线的解析式;
(3)如图,利用(1)(2)知道四边形OACD是梯形,利用已知条件可以求出其面积,设E的横坐标为x,那么利用x可以表示其纵坐标,也可以表示△OEC的面积,而△OCD的面积可以求出,所以根据四边形OECD的面积S1,是四边形OACD面积S的![]() 即可列出关于x的方程,利用方程即可解决问题.
即可列出关于x的方程,利用方程即可解决问题.
(1)∵反比例函数的图象都经过点A(3,3),
∴经过点A的反比例函数解析式为:y=![]() ,
,
而直线OA向下平移后,与反比例函数的图象交于点B(6,m),
∴m=![]() ;
;
(2)∵直线OA向下平移后,与反比例函数的图象交于点B(6,![]() ),
),
与x轴、y轴分别交于C、D两点,
而这些OA的解析式为y=x,
设直线CD的解析式为y=x+b,
代入B的坐标得:![]() =6+b,
=6+b,
∴b=-4.5,
∴直线OC的解析式为y=x-4.5,
∴C、D的坐标分别为(4.5,0),(0,-4.5),
设过A、B、D三点的抛物线的解析式为y=ax2+bx+c,
分别把A、B、D的坐标代入其中得:
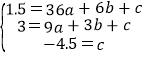 ,
,
解之得:a=-0.5,b=4,c=-4.5
∴y=-![]() x2+4x-
x2+4x-![]() ;
;
(3)如图,设E的横坐标为x,
∴其纵坐标为-0.5x2+4x-4.5,
∴S1=![]() (-0.5x2+4x-4.5+OD)×OC,
(-0.5x2+4x-4.5+OD)×OC,
=![]() (-0.5x2+4x-4.5+4.5)×4.5,
(-0.5x2+4x-4.5+4.5)×4.5,
=![]() (-0.5x2+4x)×4.5,
(-0.5x2+4x)×4.5,
而S=![]() (3+OD)×OC=
(3+OD)×OC=![]() (3+4.5)×4.5=
(3+4.5)×4.5=![]() ,
,
∴![]() (-0.5x2+4x)×4.5=
(-0.5x2+4x)×4.5=![]() ×
×![]() ,
,
解之得x=4±![]() ,
,
∴这样的E点存在,坐标为(4-![]() ,
,![]() ),(4+
),(4+![]() ,
,![]() ).
).

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案