题目内容
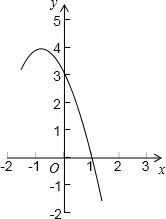
已知抛物线y=-x2+bx+c的图象经过（1，0）和（0，3）两点，它的部分图象如下图．
（1）求b、c的值；
（2）写出当y＞0时，x的取值范围；
（3）求y的取值范围．
（1）求b、c的值；
（2）写出当y＞0时，x的取值范围；
（3）求y的取值范围．
（1）把（1，0）和（0，3）代入y=-x2+bx+c得，
，
解得b=-2，c=3（3分）；
（2）抛物线的解析式为：y=-x2-2x+3，
令y=0，则x=-3或1，
当y＞0时，-3＜x＜1（6分）．
（3）∵y=-x2-2x+3，∴y=-（x+1）2+4，
∴抛物线的顶点坐标（-1，4）
∴y≤4（10分）．
|
解得b=-2，c=3（3分）；
（2）抛物线的解析式为：y=-x2-2x+3，
令y=0，则x=-3或1，
当y＞0时，-3＜x＜1（6分）．
（3）∵y=-x2-2x+3，∴y=-（x+1）2+4，
∴抛物线的顶点坐标（-1，4）
∴y≤4（10分）．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
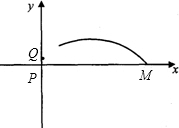
的长是方程x2-6x+5=0的两个实数根．
