题目内容
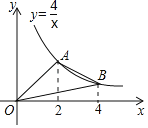
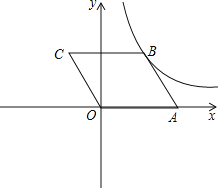
【题目】如图,在平面直角坐标系中,![]() OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数
OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数![]() 的图像经过点B.
的图像经过点B.
(1)求k的值.
(2)将![]() OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数
OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数![]() 的图像上,请通过计算说明理由.
的图像上,请通过计算说明理由.
【答案】(1)2(2)在,理由见解析
【解析】
(1)根据平行四边形的性质可得AO=BC,再根据A、C点坐标可以算出B点坐标,再把B点坐标代入反比例函数解析式中即可求出k的值.
(2)根据翻折方法可知C与C′点关于x轴对称,故C′点坐标是(-1,-2),把C′点坐标(-1,-2)代入解析式发现能使解析式左右相等,故点C′是否在反比例函数的图象上
解:(1)∵四边形OABC是平行四边形,
∴BC=AO,
∵A(2,0),
∴OA=2,
∴BC=2,
∵C(-1,2),
∴CD=1,
∴BD=BC-CD=2-1=1,
∴B(1,2),
∵反比例函数y=![]() (k≠0)的图象经过点B,
(k≠0)的图象经过点B,
∴k=1×2=2;
(2)∵OABC沿x轴翻折,点C落在点C′处,
∴C′点坐标是(-1,-2),
∵k=2,
∴反比例函数解析式为y=![]() ,
,
把C′点坐标(-1,-2)代入函数解析式能使解析式左右相等,
故点C′在反比例函数y=![]() 的图象上.
的图象上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
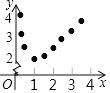
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .