Question

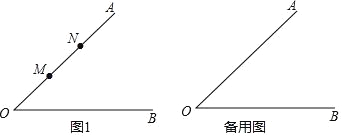
【题目】如图，∠AOB=45°，点M，N在边OA上，点P是边OB上的点．

（1）利用直尺和圆规在图1确定点P，使得PM=PN；

（2）设OM=x，ON=x+4，

①若x=0时，使P、M、N构成等腰三角形的点P有　　个；

②若使P、M、N构成等腰三角形的点P恰好有三个，则x的值是____________．

Answer 1

【答案】（1）见解析；（2）①3；②：x=0或x=4﹣4或4＜x＜4；

【解析】

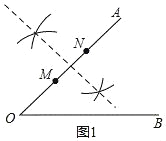
（1）分别以M、N为圆心，以大于MN为半径作弧，两弧相交与两点，过两弧交

点的直线就是MN的垂直平分线；

（2）①分为PM=PN，MP=MN，NP=NM三种情况进行判断即可；②如图3，构建腰长为4

的等腰直角△OMC，和半径为4的⊙M，发现M在点D的位置时，满足条件；如图4，根

据等腰三角形三种情况的画法：分别以M、N为圆心，以MN为半径画弧，与OB的交点就

是满足条件的点P，再以MN为底边的等腰三角形，通过画图发现，无论x取何值，以MN

为底边的等腰三角形都存在一个，所以只要满足以MN为腰的三角形有两个即可．

（1）如图所示：

（2）①如图所示：

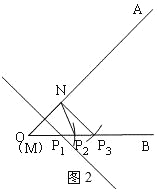
故答案为：3．

②如图3，以M为圆心，以4为半径画圆，当⊙M与OB相切时，设切点为C，⊙M与OA交于D，

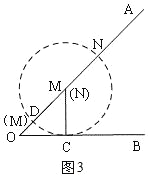
∴MC⊥OB，

∵∠AOB=45°，

∴△MCO是等腰直角三角形，

∴MC=OC=4，

∴

当M与D重合时，即时，同理可知：点P恰好有三个；

如图4，取OM=4，以M为圆心，以OM为半径画圆．

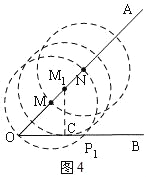
则⊙M与OB除了O外只有一个交点，此时x=4，即以∠PMN为顶角，MN为腰，符合条件的点P有一个，以N圆心，以MN为半径画圆，与直线OB相离，说明此时以∠PNM为顶角，以MN为腰，符合条件的点P不存在，还有一个是以NM为底边的符合条件的点P；

点M沿OA运动，到M1时，发现⊙M1与直线OB有一个交点；

∴当时，圆M在移动过程中，则会与OB除了O外有两个交点，满足点P恰好有三个；

综上所述，若使点P，M，N构成等腰三角形的点P恰好有三个，则x的值是：x=0或或

故答案为：x=0或或