��Ŀ����
����Ŀ��(1)���ⷢ��
��ͼ1,��ACB����DCE��Ϊ����ֱ��������,��ACB=90��,B,C,D��һ��ֱ����.
���:�߶�AD,BE֮��Ĺ�ϵΪ .
(2)��չ̽��
��ͼ2,��ACB����DCE��Ϊ����ֱ��������,��ACB=��DCE=90��,���ж�AD,BE�Ĺ�ϵ,��˵������.
(3)�������
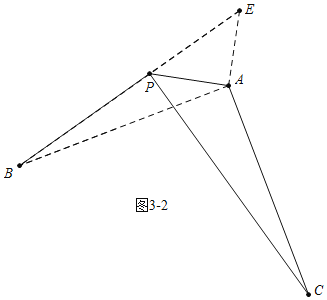
��ͼ3,�߶�PA=3,��B���߶�PA��һ��,PB=5,����AB,��AB�Ƶ�A��ʱ����ת90��õ��߶�AC,���ŵ�B��λ�õı仯,ֱ��д��PC�ķ�Χ.

���𰸡�(1) AD=BE��AD��BE��(2) AD=BE��AD��BE��(3) 5-3![]() ��PC��5+3
��PC��5+3![]() ��
��
��������
��1�����ݵ�������������֤��ACD�ա�BCE��SAS������AD=BE����EBC=��CAD���ӳ�BE��AD�ڵ�F���ɴ�ֱ�����AD��BE��
��2�����ݵ�������������֤��ACD�ա�BCE��SAS����AD=BE����CAD=��CBE���ɴ�ֱ����á�OHB=90����AD��BE��
��3����AE��AP��ʹ��AE=PA������֤��APE�ա�ACP��PC=BE����P��E��B����ʱ��BE��С����Сֵ=PB-PE����P��E��B����ʱ��BE������ֵ=PB+PE����5-3![]() ��BE��5+3
��BE��5+3![]() .
.
��1�����ۣ�AD=BE��AD��BE��
���ɣ���ͼ1�У�
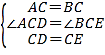
�ߡ�ACB���DCE��Ϊ����ֱ�������Σ�
��AC=BC��CE=CD��
��ACB=��ACD=90����
��Rt��ACD��Rt��BCE��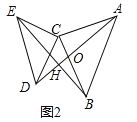
���ACD�ա�BCE��SAS����
��AD=BE����EBC=��CAD
�ӳ�BE��AD�ڵ�F��
��BC��AD��
���EBC+��CEB=90����
�ߡ�CEB=AEF��
���EAD+��AEF=90����
���AFE=90������AD��BE��
��AD=BE��AD��BE��
�ʴ�ΪAD=BE��AD��BE��
��2�����ۣ�AD=BE��AD��BE��
���ɣ���ͼ2�У���AD��BE��H��AD��BC��O��

�ߡ�ACB���DCE��Ϊ����ֱ�������Σ�
��AC=BC��CE=CD����ACB=��ECD=90����
��ACD=��BCE��
��Rt��ACD��Rt��BCE�� ��
��
���ACD�ա�BCE��SAS����
��AD=BE����CAD=��CBE��
�ߡ�CAO+��AOC=90������AOC=��BOH��
���BOH+��OBH=90����
���OHB=90����
��AD��BE��
��AD=BE��AD��BE��
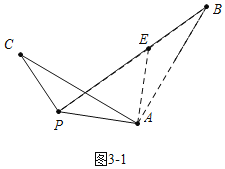
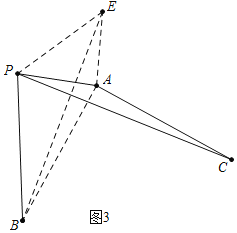
��3����ͼ3�У���AE��AP��ʹ��AE=PA������֤��APE�ա�ACP��
��PC=BE��
ͼ3-1�У���P��E��B����ʱ��BE��С����Сֵ=PB-PE=5-3![]() ��
��
ͼ3-2�У���P��E��B����ʱ��BE������ֵ=PB+PE=5+3![]() ��
��
��5-3![]() ��BE��5+3
��BE��5+3![]() ��
��
��5-3![]() ��PC��5+3
��PC��5+3![]() ��
��