题目内容
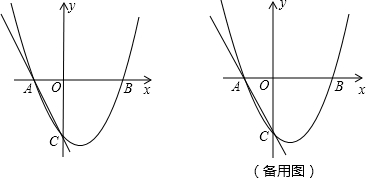
（2012•宁波）如图，二次函数y=ax2+bx+c的图象交x轴于A（-1，0），B（2，0），交y轴于C（0，-2），过A，C画直线．
（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长；
（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．
①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；
②若⊙M的半径为
，求点M的坐标．
（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长；
（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．
①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；
②若⊙M的半径为
| 4 |
| 5 |
| 5 |
分析：（1）根据与x轴的两个交点A、B的坐标，设出二次函数交点式解析式y=a（x+1）（x-2），然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式；
（2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可；
（3）①根据相似三角形对应角相等可得∠MCH=∠CAO，然后分（i）点H在点C下方时，利用同位角相等，两直线平行判定CM∥x轴，从而得到点M的纵坐标与点C的纵坐标相同，是-2，代入抛物线解析式计算即可；（ii）点H在点C上方时，根据（2）的结论，点M为直线PC与抛物线的另一交点，求出直线PC的解析式，与抛物线的解析式联立求解即可得到点M的坐标；
②在x轴上取一点D，过点D作DE⊥AC于点E，可以证明△AED和△AOC相似，根据相似三角形对应边成比例列式求解即可得到AD的长度，然后分点D在点A的左边与右边两种情况求出OD的长度，从而得到点D的坐标，再作直线DM∥AC，然后求出直线DM的解析式，与抛物线解析式联立求解即可得到点M的坐标．
（2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可；
（3）①根据相似三角形对应角相等可得∠MCH=∠CAO，然后分（i）点H在点C下方时，利用同位角相等，两直线平行判定CM∥x轴，从而得到点M的纵坐标与点C的纵坐标相同，是-2，代入抛物线解析式计算即可；（ii）点H在点C上方时，根据（2）的结论，点M为直线PC与抛物线的另一交点，求出直线PC的解析式，与抛物线的解析式联立求解即可得到点M的坐标；
②在x轴上取一点D，过点D作DE⊥AC于点E，可以证明△AED和△AOC相似，根据相似三角形对应边成比例列式求解即可得到AD的长度，然后分点D在点A的左边与右边两种情况求出OD的长度，从而得到点D的坐标，再作直线DM∥AC，然后求出直线DM的解析式，与抛物线解析式联立求解即可得到点M的坐标．
解答：解：（1）设该二次函数的解析式为：y=a（x+1）（x-2），
将x=0，y=-2代入，得-2=a（0+1）（0-2），
解得a=1，
∴抛物线的解析式为y=（x+1）（x-2），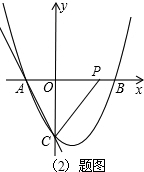
即y=x2-x-2；
（2）设OP=x，则PC=PA=x+1，
在Rt△POC中，由勾股定理，得x2+22=（x+1）2，
解得，x=
，
即OP=
；
（3）①∵△CHM∽△AOC，
∴∠MCH=∠CAO，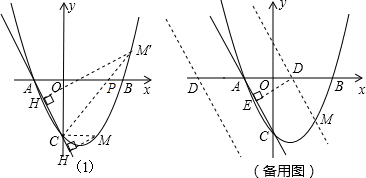
（i）如图1，当H在点C下方时，
∵∠MCH=∠CAO，
∴CM∥x轴，
∴yM=-2，
∴x2-x-2=-2，
解得x1=0（舍去），x2=1，
∴M（1，-2），
（ii）如图1，当H在点C上方时，
∵∠MCH=∠CAO，
∴PA=PC，由（2）得，M′为直线CP与抛物线的另一交点，
设直线CM的解析式为y=kx-2，
把P（
，0）的坐标代入，得
k-2=0，
解得k=
，
∴y=
x-2，
由
x-2=x2-x-2，
解得x1=0（舍去），x2=
，
此时y=
×
-2=
，
∴M′（
，
），
②在x轴上取一点D，如图（备用图），过点D作DE⊥AC于点E，使DE=
，
在Rt△AOC中，AC=
=
=
，
∵∠COA=∠DEA=90°，∠OAC=∠EAD，
∴△AED∽△AOC，
∴
=
，
即
=
，
解得AD=2，
∴D（1，0）或D（-3，0）．
过点D作DM∥AC，交抛物线于M，如图（备用图）
则直线DM的解析式为：y=-2x+2或y=-2x-6，
当-2x-6=x2-x-2时，即x2+x+4=0，方程无实数根，
当-2x+2=x2-x-2时，即x2+x-4=0，解得x1=
，x2=
，
∴点M的坐标为（
，3+
）或（
，3-
）．
将x=0，y=-2代入，得-2=a（0+1）（0-2），
解得a=1，
∴抛物线的解析式为y=（x+1）（x-2），
即y=x2-x-2；
（2）设OP=x，则PC=PA=x+1，
在Rt△POC中，由勾股定理，得x2+22=（x+1）2，
解得，x=
| 3 |
| 2 |
即OP=
| 3 |
| 2 |
（3）①∵△CHM∽△AOC，
∴∠MCH=∠CAO，
（i）如图1，当H在点C下方时，
∵∠MCH=∠CAO，
∴CM∥x轴，
∴yM=-2，
∴x2-x-2=-2，
解得x1=0（舍去），x2=1，
∴M（1，-2），
（ii）如图1，当H在点C上方时，
∵∠MCH=∠CAO，
∴PA=PC，由（2）得，M′为直线CP与抛物线的另一交点，
设直线CM的解析式为y=kx-2，
把P（
| 3 |
| 2 |
| 3 |
| 2 |
解得k=
| 4 |
| 3 |
∴y=
| 4 |
| 3 |
由
| 4 |
| 3 |
解得x1=0（舍去），x2=
| 7 |
| 3 |
此时y=
| 4 |
| 3 |
| 7 |
| 3 |
| 10 |
| 9 |
∴M′（
| 7 |
| 3 |
| 10 |
| 9 |
②在x轴上取一点D，如图（备用图），过点D作DE⊥AC于点E，使DE=
4
| ||
| 5 |
在Rt△AOC中，AC=
| AO2+CO2 |
| 12+22 |
| 5 |
∵∠COA=∠DEA=90°，∠OAC=∠EAD，
∴△AED∽△AOC，
∴
| AD |
| AC |
| DE |
| OC |
即
| AD | ||
|
| ||||
| 2 |
解得AD=2，
∴D（1，0）或D（-3，0）．
过点D作DM∥AC，交抛物线于M，如图（备用图）
则直线DM的解析式为：y=-2x+2或y=-2x-6，
当-2x-6=x2-x-2时，即x2+x+4=0，方程无实数根，
当-2x+2=x2-x-2时，即x2+x-4=0，解得x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∴点M的坐标为（
-1-
| ||
| 2 |
| 17 |
-1+
| ||
| 2 |
| 17 |
点评：本题是对二次函数的综合考查，主要利用了待定系数法求二次函数解析式，勾股定理，相似三角形的性质，两函数图象交点的求解方法，综合性较强，难度较大，要注意分情况讨论求解．
练习册系列答案
快乐5加2金卷系列答案
相关题目
（2012•宁波）如图，在△ABC中，BE是它的角平分线，∠C=90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F．
（2012•宁波）如图，已知一次函数与反比例函数的图象交于点A（-4，-2）和B（a，4）．
（2012•宁波）如图是某物体的三视图，则这个物体的形状是（ ）
（2012•宁波）如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=2