题目内容
【题目】阅读下列材料:
如图1,在线段AB上找一点C(AC>BC),若BC:AC=AC:AB,则称点C为线段AB的黄金分割点,这时比值为![]() ≈0.618,人们把
≈0.618,人们把![]() 称为黄金分割数.长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
称为黄金分割数.长期以来,很多人都认为黄金分割数是一个很特别的数,我国著名数学家华罗庚先生所推广的优选法中,就有一种0.618法应用了黄金分割数.
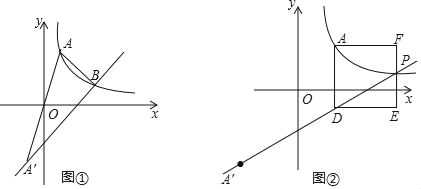
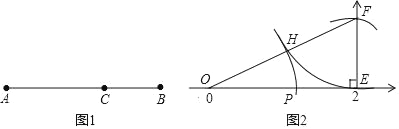
我们可以这样作图找到已知线段的黄金分割点:如图2,在数轴上点O表示数0,点E表示数2,过点E作EF⊥OE,且EF=![]() OE,连接OF;以F为圆心,EF为半径作弧,交OF于H;再以O为圆心,OH为半径作弧,交OE于点P,则点P就是线段OE的黄金分割点.
OE,连接OF;以F为圆心,EF为半径作弧,交OF于H;再以O为圆心,OH为半径作弧,交OE于点P,则点P就是线段OE的黄金分割点.
根据材料回答下列问题:(1)线段OP长为_____,点P在数轴上表示的数为_____;(2)在(1)中计算线段OP长的依据是_____.
【答案】(1)![]() ﹣1,
﹣1, ![]() ﹣1; (2)勾股定理.
﹣1; (2)勾股定理.
【解析】
(1)根据勾股定理得到OF=![]() ,根据线段的和差即可得到结论;(2)根据勾股定理求得OF,再由线段的和差求得OP,于是得到结论.
,根据线段的和差即可得到结论;(2)根据勾股定理求得OF,再由线段的和差求得OP,于是得到结论.
(1)∵OE=2,
∴EF=![]() OE=1,
OE=1,
∵EF⊥OE,
∴OF=![]() ,
,
由作法知,FH=EF=1,OP=OH=OF-FH=![]() -1,
-1,
∴点P在数轴上表示的数为:![]() -1,
-1,
故答案为:![]() -1,
-1,![]() -1;
-1;
(2)在(1)中计算线段OP长时,
首先根据勾股定理求得OF,
再由OP=OH=OF-FH求得OP,
故答案为:勾股定理.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少![]() .
.
A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格 | 1100 | 1400 |
销售价格 | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?