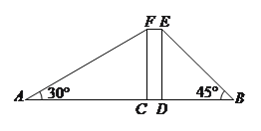
题目内容
【题目】如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
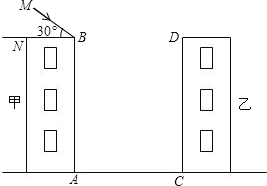
【答案】投到乙楼影子高度是16.14m
【解析】试题分析:
(1)首先要作出甲楼投到乙楼的影子,如下图所示,线段CE即表示乙楼的影子;
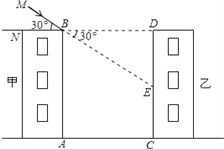
(2)求甲楼投在乙楼上的影子的高度即需求线段CE的长,为此,必须要求出DE的长,而DE为Rt△DEB的边长,且楼间距AC=BD=24m,∠DBE=30°,所以解这个直角三角形即可求解.
解:如图,延长MB交CD于E,连接BD,
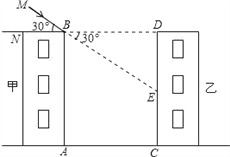
由于AB=CD=30m,AB⊥AC,CD⊥AC,
∴四边形ACDB是矩形,
∴NB和BD在同一直线上,∠DBE=∠MBN=30°
∴AC=BD=24m,∠BDE=90°,
在Rt△BED中tan30°=![]() ,
,
DE=BDtan30°=24×![]() ,
,
∴CE=30﹣8![]() ≈16.14(m),
≈16.14(m),
答:甲楼投到乙楼影子高度是16.14m.

练习册系列答案
相关题目