Question

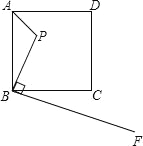
【题目】如图，已知点P是边长为5的正方形ABCD内一点，且PB＝3，BF⊥BP于B，若在射线BF上找一点M，使以点B，M，C为顶点的三角形与△ABP相似，BM的值为（ ）

A. 3 B. C. 3或 D. 3或5

Answer 1

【答案】C

【解析】

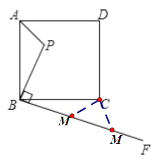
由于∠ABC=∠PBF=90°，同时减去∠PBC后可得到∠ABP=∠CBF，若以点B，M，C为顶点的三角形与△ABP相似，那么必有：AB：PB=BC：BM或AB：BP=BM：BC，可据此求得BM的值．

∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC=5；
又∵∠PBF=90°，
∴∠ABP=∠CBF=90°-∠CBP；
若以点B，M，C为顶点的三角形与△ABP相似，
则：①，即，解得BM= ；
②，即，解得BM=3；
故选C．