题目内容
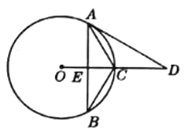
【题目】如图,在△ABC中,D是BC边上一点,E是AC边上一点.且满足AD=AB,∠ADE=∠C.
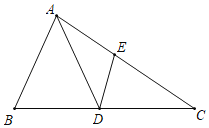
(1)求证:AB2=AEAC;
(2)若D为BC中点,AE=4,EC=6,且tanB=3,求△ABC的面积.
【答案】(1)见解析;(2)S△ABC=24
【解析】
(1)由题意可证△ADE∽△ACD,可得![]() ,可得结论;
,可得结论;
(2)过点A作AH⊥BC,垂足为H,先求AB的长,由锐角三角函数可求AH,BH的长,即可求BD,BC的长,由三角形面积公式可求解.
(1)∵∠ADE=∠C,∠DAE=∠DAC,
∴△ADE∽△ACD
∴![]()
∵AB=AD
∴AB2=AEAC
(2)过点A作AH⊥BC,垂足为H,
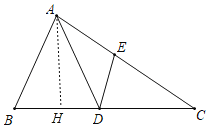
∵AB2=AEAC
∴AB=2![]()
在Rt△ABH中,∠AHB=90°,tanB=3
∴AH=6,BH=2
∴BH=DH=2
∴BD=4
∵D是中点
∴BC=8
∴S△ABC=![]() ×BC×AH=24
×BC×AH=24

练习册系列答案
相关题目