题目内容
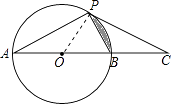
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°. 
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.
【答案】
(1)证明:连接OP,如图所示:
∵PA=PC,∠C=30°,
∴∠A=∠C=30°,
∴∠APC=120°,
∵OA=OP,
∴∠OPA=∠A=30°,
∴∠OPC=120°﹣30°=90°,
即OP⊥CP,
∴CP是⊙O的切线.
(2)解:∵AB是⊙O的直径,
∴∠APB=90°,
∴∠OBP=90°﹣∠A=60°,
∵OP=OB=4,
∴△OBP是等边三角形,
∴阴影部分的面积=扇形OBP的面积﹣△OBP的面积= ![]() ﹣
﹣ ![]() ×4×2
×4×2 ![]() =
= ![]() ﹣4
﹣4 ![]() .
.
【解析】(1)连接OP,由等腰三角形的性质得出∠C=∠OPA=30°,∠APC=120°,求出∠OPC=90°即可;(2)证明△OBP是等边三角形,阴影部分的面积=扇形OBP的面积﹣△OBP的面积,即可得出结果.本题考查的是切线的判定、等腰三角形的性质、圆周角定理、等边三角形的判定与性质、扇形面积公式等知识;熟练掌握切线的判定.证明三角形是等边三角形是解决问题(2)的关键.

练习册系列答案
相关题目










