题目内容
若△ABC的周长为l，两条内角平分线的交点到一边的距离为r，那么△ABC的面积为分析：设该三角形的内心是点I，连接IA、IB、IC．根据三角形的面积等于分割成的三部分的面积进行计算．
解答：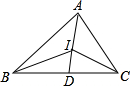
解：设该三角形的内心是点I，连接IA、IB、IC．
根据题意，得
（AB+BC+AC）•r=S，
S=
lr．
解：设该三角形的内心是点I，连接IA、IB、IC．根据题意，得
| 1 |
| 2 |
S=
| 1 |
| 2 |
点评：此题考查了三角形的内心的性质：三角形的内心到三角形的三个顶点的距离相等．
练习册系列答案
备战中考寒假系列答案
相关题目
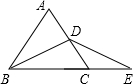在等边△ABC中，D为AC的中点，E为BC延长线上一点，且DB=DE，若△ABC的周长为12，则△DCE的周长为（ ）| A、4 | ||
B、4+2
| ||
C、4+
| ||
D、4+2
|
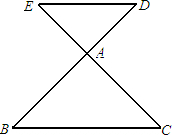如图：已知DE∥BC，DE=2，BC=3，若△ABC的周长为8，则△ADE的周长为
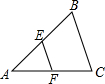如图，在△ABC中，点E、F分别为AB、AC的中点．若△ABC的周长为6，则△AEF的周长为（ ）
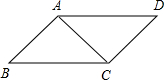如图所示，在?ABCD中，已知AC=3cm，若△ABC的周长为8cm，则平行四边形的周长为（ ）