Question

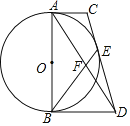
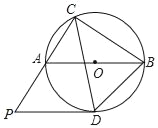
【题目】如图，△ABC内接于⊙O，AB⊙O的直径，∠ACB的平分线交⊙O于D，连接AD和BD，过点D作DP∥AB交CA的延长线于P．

（1）求证：PD是⊙O的切线；

（2）当AC＝6，BC＝8时，求CD的长．

Answer 1

【答案】（1）详见解析；（2）7.

【解析】

（1）欲证明PD是⊙O的切线，只要证明OD⊥PD即可；

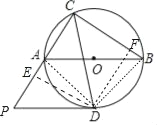
（2）如图2中，连接AD、BD，作DE⊥CP与E，DF⊥BC于F．只要证明四边形DECF是正方形且边长为7，即可解决问题；

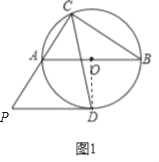
（1）证明：如图1中，连接OD．

∵∠DCA=∠DCB，

∴OD⊥AB，

∵AB∥PD，

∴OD⊥PD，

∴PD是⊙O的切线．

（2）如图2中，连接AD、BD，作DE⊥CP与E，DF⊥BC于F．

∵AB是直径，

∴∠ECF=∠CED=∠CFD=90°，

∴四边形DECF是矩形，

∵DC平分∠ACB，DE⊥CA，DF⊥CB，

∴DE=DF，

∴四边形DECF是正方形，

∵∵∠DCA=∠DCB，

∴AD=BD，

∴ AE=BF，

∴ CE+CF=AC+AE+CB﹣BF=AC+BC=14，

∴ CE=CF=DE=DF=7，

∴CD=CE=7．