题目内容
已知E为正方形ABCD对角线AC上一点(不与A,C重合),将△BCE逆时针旋转可得到△BAF,连接EF.
(1)请指出旋转中心为点______,旋转角为______°;
(2)下列四个结论均为正确结论:①AF=CE;②∠1=∠2;③△BEF为等腰直角三角形;④AE⊥AF;请你选择其中一个结论给予证明.
(3)若AE=5,EF比CE大1,求△AEF的面积.
(1)请指出旋转中心为点______,旋转角为______°;
(2)下列四个结论均为正确结论:①AF=CE;②∠1=∠2;③△BEF为等腰直角三角形;④AE⊥AF;请你选择其中一个结论给予证明.
(3)若AE=5,EF比CE大1,求△AEF的面积.

(1)∵将△BCE逆时针旋转可得到△BAF,此时AB与BC重合,
∴旋转中心为点B,旋转角为90°;
故答案为:B,90;
(2)四个结论利用旋转的性质都比较容易证出,以证明④AE⊥AF为例:

证明:∵E为正方形ABCD对角线AC上一点,
∴∠2=∠BAC=45°,
∵将△BCE逆时针旋转可得到△BAF,
∴∠2=∠1=45°,
∴FAE=∠1+∠BAC=45°+45°=90°,
∴AE⊥AF;
(3)∵将△BCE逆时针旋转可得到△BAF,
∴AF=EC,
∵AE=5,EF比CE大1,
∴设EC=x,则AF=x,EF=x+1,
∴在Rt△FAE中,AF 2+AE 2=EF 2,
则x 2+5 2=(x+1) 2,
解得:x=12,
故△AEF的面积为:
×AE×AF=
×5×12=30.
∴旋转中心为点B,旋转角为90°;
故答案为:B,90;
(2)四个结论利用旋转的性质都比较容易证出,以证明④AE⊥AF为例:

证明:∵E为正方形ABCD对角线AC上一点,
∴∠2=∠BAC=45°,
∵将△BCE逆时针旋转可得到△BAF,
∴∠2=∠1=45°,
∴FAE=∠1+∠BAC=45°+45°=90°,
∴AE⊥AF;
(3)∵将△BCE逆时针旋转可得到△BAF,
∴AF=EC,
∵AE=5,EF比CE大1,
∴设EC=x,则AF=x,EF=x+1,
∴在Rt△FAE中,AF 2+AE 2=EF 2,
则x 2+5 2=(x+1) 2,
解得:x=12,
故△AEF的面积为:
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目

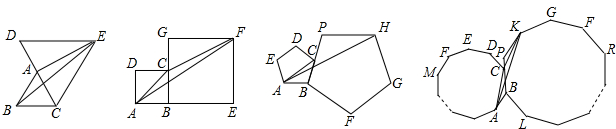
 我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.