题目内容
已知AB=2| 3 |
(1)求DE的取值范围;
(2)当DE在什么范围取值时,△ABH为钝角三角形;
(3)过B、A、G三点的圆与BC相交于点K,过K作这个圆的切线KL与DG的延长线相交于点L.若GL=1,这时点K与点F重合吗?请说明理由.
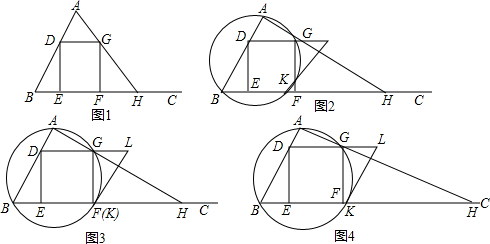
分析:(1)当D与B重合时,DE最小为0,当D与A重合时,DE最大,可根据AB和∠B的度数用正弦函数求出DE的最大值,即可得出DE的取值范围;
(2)要分两种情况进行讨论:
①当∠BAH是钝角时,此时DE的最小值就应该是∠BAH=90°时的值,DE的最大值就是(1)中求得的DE的最大值,当∠BAH=90°时,可用DE在直角三角形BDE和ADG中分别表示出AD,BD,然后根据AB的值求出DE的值,也就求出了∠BAH是钝角时,DE的取值范围;
②当∠AHB为钝角时,此时DE的最大值就应该是H与F重合时DE的值,参照上面的方法求出DE的值,也就求出了∠AHB是钝角时DE的取值范围,
然后结合(1)中DE的取值范围就能得出三角形ABH是钝角三角形时DE的范围;
(3)假设他们重合,此时四边形AGFB就是圆的内接四边形,那么外角∠GFC=∠=90°,这种情况和(2)中①求DE最小值时的情况完全一样,我们已经得出了此时DE,BE的值,那么就求出了BF,GF,DG的长,然后我们通过构建相似三角形来判断GL是否等于1,连接BG后我们发现弦切角∠LKG=∠GBK,因此三角形GKL与BFG相似,那么可得出BF、GF、GL的比例关系,根据求出的BF、GF的值即可求出GL的值,看看是否与已知的条件相符即可.
(2)要分两种情况进行讨论:
①当∠BAH是钝角时,此时DE的最小值就应该是∠BAH=90°时的值,DE的最大值就是(1)中求得的DE的最大值,当∠BAH=90°时,可用DE在直角三角形BDE和ADG中分别表示出AD,BD,然后根据AB的值求出DE的值,也就求出了∠BAH是钝角时,DE的取值范围;
②当∠AHB为钝角时,此时DE的最大值就应该是H与F重合时DE的值,参照上面的方法求出DE的值,也就求出了∠AHB是钝角时DE的取值范围,
然后结合(1)中DE的取值范围就能得出三角形ABH是钝角三角形时DE的范围;
(3)假设他们重合,此时四边形AGFB就是圆的内接四边形,那么外角∠GFC=∠=90°,这种情况和(2)中①求DE最小值时的情况完全一样,我们已经得出了此时DE,BE的值,那么就求出了BF,GF,DG的长,然后我们通过构建相似三角形来判断GL是否等于1,连接BG后我们发现弦切角∠LKG=∠GBK,因此三角形GKL与BFG相似,那么可得出BF、GF、GL的比例关系,根据求出的BF、GF的值即可求出GL的值,看看是否与已知的条件相符即可.
解答:解:(1)当点D与点A重合时,
在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=2
,
∴AE=DE=AB•sin∠ABE=2
•sin60°=2
×
=3,
当点D与B重合时,DE=0,
∴DE的取值范围是:0<DE<3;
(2)设BE=x,Rt△BDE中,
∵∠ABE=60°,则BD=2x,DE=
x,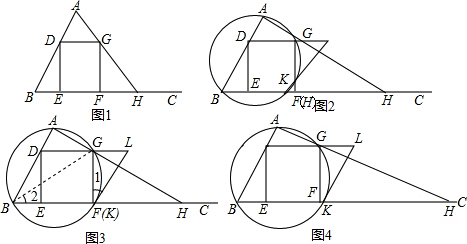
分两种情况:
①若∠BAH=90°,如图1
在Rt△ADG中,∠ADG=∠ABE=60°,DG=DE=
x
∴AD=
x,又AB=AD+BD=2
,
∴2x+
x=2
,x=
,
∴DE=
x=
,
即当
<DE<3时,△ABH为钝角三角形.
②若∠AHB=90°,如图2,此时点F与点H重合.
在Rt△ADG中,∠ADG=∠ABE=60°,DG=DE=
x,
∴AD=2
x,又AB=AD+BD=2
,
∴2x+2
x=2
∴x=
,
∴DE=
x=
,
则当0<DE<
时,△ABH为钝角三角形.
综上,当
<DE<3或0<DE<
时,△ABH为钝角三角形;
(3)当GL=1时,点K与点F不重合,理由如下:
解:当点K与点F重合时,如图3,
∵四边形ABKG内接于圆,
∴∠A+∠BKG=180°,
∵∠BKG=90°,
∴∠A=90°,
∴此时即为(2)中①的情形,仍然设BE=x,则DE=GK=EK=
x,
∴BK=BE+EK=x+
x=(
+1)x,
在(2)①中已求得:x=
.
连接BG,∵KL切圆于点K,
∴∠1=∠2,
又∵∠KGL=∠BKG=90°,
∴△GKL∽△KBG,
∴
=
,
∴GL=
=
=
x=
﹒
≠1,
∴当GL=1时,点K与点F不重合.
在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=2
| 3 |
∴AE=DE=AB•sin∠ABE=2
| 3 |
| 3 |
| ||
| 2 |
当点D与B重合时,DE=0,
∴DE的取值范围是:0<DE<3;
(2)设BE=x,Rt△BDE中,
∵∠ABE=60°,则BD=2x,DE=
| 3 |

分两种情况:
①若∠BAH=90°,如图1
在Rt△ADG中,∠ADG=∠ABE=60°,DG=DE=
| 3 |
∴AD=
| ||
| 2 |
| 3 |
∴2x+
| ||
| 2 |
| 3 |
16
| ||
| 13 |
∴DE=
| 3 |
48-12
| ||
| 13 |
即当
48-12
| ||
| 13 |
②若∠AHB=90°,如图2,此时点F与点H重合.
在Rt△ADG中,∠ADG=∠ABE=60°,DG=DE=
| 3 |
∴AD=2
| 3 |
| 3 |
∴2x+2
| 3 |
| 3 |
∴x=
3-
| ||
| 2 |
∴DE=
| 3 |
3
| ||
| 2 |
则当0<DE<
3
| ||
| 2 |
综上,当
48-12
| ||
| 13 |
3
| ||
| 2 |
(3)当GL=1时,点K与点F不重合,理由如下:
解:当点K与点F重合时,如图3,
∵四边形ABKG内接于圆,
∴∠A+∠BKG=180°,
∵∠BKG=90°,
∴∠A=90°,
∴此时即为(2)中①的情形,仍然设BE=x,则DE=GK=EK=
| 3 |
∴BK=BE+EK=x+
| 3 |
| 3 |
在(2)①中已求得:x=
16
| ||
| 13 |
连接BG,∵KL切圆于点K,
∴∠1=∠2,
又∵∠KGL=∠BKG=90°,
∴△GKL∽△KBG,
∴
| GL |
| GK |
| GK |
| BK |
∴GL=
| GK2 |
| BK |
(
| ||
(
|
3
| ||
| 2 |
3
| ||
| 2 |
16
| ||
| 13 |
∴当GL=1时,点K与点F不重合.
点评:本题主要考查了切线的性质,正方形的性质,解直角三角形以及相似三角形的判断和性质等知识点,由于涉及的知识点较多,此题比较难.

练习册系列答案
相关题目
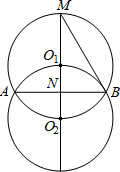 于点N,连接BM,已知AB=2
于点N,连接BM,已知AB=2
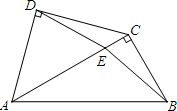 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2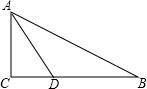 在△ABC中,∠C=90°,∠CAB=60°,AD是∠BAC的平分线,已知AB=2
在△ABC中,∠C=90°,∠CAB=60°,AD是∠BAC的平分线,已知AB=2