题目内容
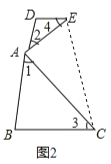
【题目】如图，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.
(1)如图①，求证：DE∥BC；
(2)若将图①改变为图②，其他条件不变，(1)中的结论是否仍成立？请说明理由．
如图，∠EAC＝90°，∠1＋∠2＝90°，∠1＝∠3，∠2＝∠4.
(1)如图①，求证：DE∥BC；
(2)若将图①改变为图②，其他条件不变，(1)中的结论是否仍成立？请说明理由．
【答案】见解析
【解析】分析：(1)用三角形的内角和定理判断∠D＋∠B＝180°；(2)连接EC，证明∠AEC＋∠ACE＋∠3＋∠4＝180°，根据同旁内角互补，两直线平行证明.
详解：(1)∵∠1＝∠3，∠2＝∠4，∴∠1＋∠3＋∠2＋∠4＝2(∠1＋∠2)，
∵∠1＋∠2＝90°，∴∠1＋∠3＋∠2＋∠4＝180°；
∵∠D＋∠B＋∠1＋∠3＋∠2＋∠4＝360°，∴∠D＋∠B＝180°，
∴DE∥BC．
(2)成立．
如图2，连接EC；
∵∠1＝∠3，∠2＝∠4，且∠1＋∠2＝90°，∴∠3＋∠4＝∠1＋∠2＝90°；
∵∠EAC＝90°，∴∠AEC＋∠ACE＝180°－90°＝90°，
∴∠AEC＋∠ACE＋∠3＋∠4＝180°，
∴DE∥BC，
即(1)中的结论仍成立．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
