��Ŀ����
����Ŀ����ͼ��ʾ�Ƕ�������·�ڿ������������ij������ʻ��·��s��km����ʱ��t�����ӣ��ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ������������⣺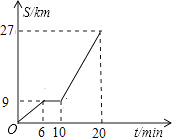
��1��������ǰ6�����ڵ�ƽ���ٶ���ǧ��/Сʱ���������˹�������ͣ�˶ʱ�䣿���ӣ�
��2����10��t��20ʱ����S��t�ĺ�����ϵʽ��
��3���涨�����ٹ�·ʱ�ٳ���120ǧ��/СʱΪ������ʻ�����жϵ�10��t��20ʱ���������Ƿ��٣�˵�����ɣ�
���𰸡�
��1��90,4
��2���⣺��S��t�ĺ�����ϵʽΪS=kt+b��
�ߵ㣨10��9������20��27���ڸú���ͼ���ϣ�
�� ![]() ����ã�
����ã� ![]() ��
��
�൱10��t��20ʱ��S��t�ĺ�����ϵʽΪS=1.8t��9��
��3���⣺��10��t��20ʱ�����������ٶ�Ϊ����27��9���£�20��10����60=108��ǧ��/Сʱ����
��108��120��
�൱10��t��20ʱ��������û�г��٣�
���������⣺��1��6����= ![]() Сʱ��
Сʱ��
������ǰ6�����ڵ�ƽ���ٶ�Ϊ��9�� ![]() =90��ǧ��/Сʱ����
=90��ǧ��/Сʱ����
�������˹�������ͣ����ʱ��Ϊ��10��6=4�����ӣ���
���Դ��ǣ�90��4��
��2����S��t�ĺ�����ϵʽΪS=kt+b��
�ߵ㣨10��9������20��27���ڸú���ͼ���ϣ�
�� ![]() ����ã�
����ã� ![]() ��
��
�൱10��t��20ʱ��S��t�ĺ�����ϵʽΪS=1.8t��9��
��3����10��t��20ʱ�����������ٶ�Ϊ����27��9���£�20��10����60=108��ǧ��/Сʱ����
��108��120��
�൱10��t��20ʱ��������û�г��٣�

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�