题目内容
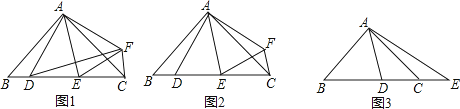
【题目】如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.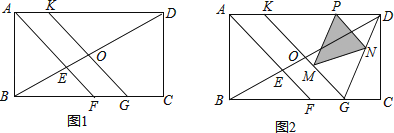
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣ ![]() .
.
①求KD的长度;
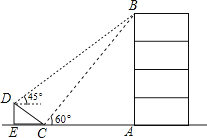
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN= ![]() 时,求m的值.
时,求m的值.
【答案】
(1)
证明:①∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
∴△DOK≌△BOG(AAS)
② 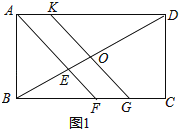
∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(2)
解:①由(1)得,四边形AFGK是平行四边形
∴AK=FG,AF=KG
又∵△DOK≌△BOG,且KD=KG
∴AF=KG=KD=BG
设AB=a,则AF=KG=KD=BG= ![]() a
a
∴AK=4﹣ ![]() ﹣
﹣ ![]() a,FG=BG﹣BF=
a,FG=BG﹣BF= ![]() a﹣a
a﹣a
∴4﹣ ![]() ﹣
﹣ ![]() a=
a= ![]() a﹣a
a﹣a
解得a= ![]()
∴KD= ![]() a=2
a=2
②过点G作GI⊥KD于点I
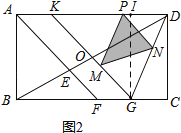
由(2)①可知KD=AF=2
∴GI=AB= ![]()
∴S△DKG= ![]() ×2×
×2× ![]() =
= ![]()
∵PD=m
∴PK=2﹣m
∵PM∥DG,PN∥KG
∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN
∴ ![]() ,即S△DPN=(
,即S△DPN=( ![]() )2×
)2× ![]()
同理S△PKM=( ![]() )2×
)2× ![]()
∵S△PMN= ![]()
∴S平行四边形PMGN=2S△PMN=2× ![]()
又∵S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM
∴2× ![]() =
= ![]() ﹣(
﹣( ![]() )2×
)2× ![]() ﹣(
﹣( ![]() )2×
)2× ![]() ,即m2﹣2m+1=0
,即m2﹣2m+1=0
解得m1=m2=1
∴当S△PMN= ![]() 时,m的值为1
时,m的值为1
【解析】(1)①先根据AAS判定△DOK≌△BOG,②再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;(2)①先根据等量代换得出AF=KG=KD=BG,再设AB=a,根据AK=FG列出关于a的方程,求得a的值,进而计算KD的长;②先过点G作GI⊥KD,求得S△DKG的值,再根据四边形PMGN是平行四边形,以及△DKG∽△PKM∽△DPN,求得S△DPN和S△PKM的表达式,最后根据等量关系S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM , 列出关于m的方程,求得m的值即可.本题主要考查了矩形的性质以及平行四边形的性质,解题时需要运用全等三角形的判定与性质.解答此题的关键是运用相似三角形的面积之比等于相似比的平方这一性质,并根据图形面积的等量关系列出方程进行求解,难度较大,具有一定的综合性.
【考点精析】本题主要考查了矩形的性质和相似三角形的判定与性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 习题精选系列答案
习题精选系列答案【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题: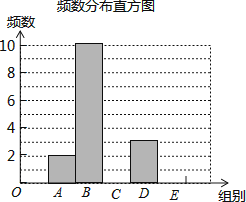
(1)填空:m= , n=
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.