题目内容
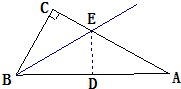 16、已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB上的一点D重合,如果要使D点恰为AB的中点,应添加什么条件?请在添加适当的条件后,给出你的证明.
16、已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB上的一点D重合,如果要使D点恰为AB的中点,应添加什么条件?请在添加适当的条件后,给出你的证明.解:添加的条件是:
∠EBD=∠A(或∠ABC=2∠A或∠A=30°)
.证明:
分析:添加的条件是:∠EBD=∠A(或∠ABC=2∠A或∠A=30°).由△BDE是由△BCE沿BE折叠而得,且点D落在AB上,即可得△BDE≌△BCE,由∠EBD=∠A,则可证得△BEA是等腰三角形,即可证得D点是AB的中点.
解答: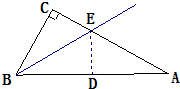 解:添加的条件是:∠EBD=∠A(或∠ABC=2∠A或∠A=30°).(1分)
解:添加的条件是:∠EBD=∠A(或∠ABC=2∠A或∠A=30°).(1分)
证明:∵△BDE是由△BCE沿BE折叠而得,且点D落在AB上,
∴△BDE≌△BCE.(2分)
∴∠BDE=∠C=90°.(3分)
又∵∠EBD=∠A,
∴△BEA是等腰三角形.(4分)
又∵∠BDE=90°,
∴D点是AB的中点.(5分)
 解:添加的条件是:∠EBD=∠A(或∠ABC=2∠A或∠A=30°).(1分)
解:添加的条件是:∠EBD=∠A(或∠ABC=2∠A或∠A=30°).(1分)证明:∵△BDE是由△BCE沿BE折叠而得,且点D落在AB上,
∴△BDE≌△BCE.(2分)
∴∠BDE=∠C=90°.(3分)
又∵∠EBD=∠A,
∴△BEA是等腰三角形.(4分)
又∵∠BDE=90°,
∴D点是AB的中点.(5分)
点评:此题考查了折叠的性质,全等三角形的判定与性质,以及等腰三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.