题目内容
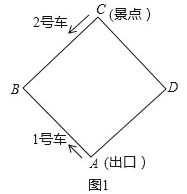
【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.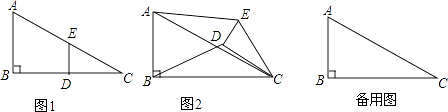
(1)问题发现
①当α=0°时, ![]() =;②当α=180°时,
=;②当α=180°时, ![]() = .
= .
(2)拓展探究
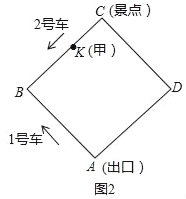
试判断:当0°≤α<360°时, ![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
【答案】
(1)![]() ;
;![]()
(2)
解:如图2,
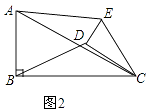 ,
,
当0°≤α<360°时, ![]() 的大小没有变化,
的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵ ![]() ,
,
∴△ECA∽△DCB,
∴ ![]()
(3)
解:①如图3,
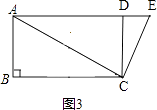 ,
,
∵AC=4 ![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD= ![]() =
= ![]() ,
,
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴ ![]() .
.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
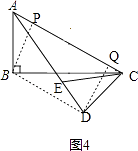 ,
,
∵AC=4 ![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD= ![]() =
= ![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴DE= ![]() =2,
=2,
∴AE=AD﹣DE=8﹣2=6,
由(2),可得
![]() ,
,
∴BD= ![]() =
= ![]() .
.
综上所述,BD的长为4 ![]() 或
或 ![]()
【解析】解:(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC= ![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴ ![]() ,
,
∴ ![]() .
.
②如图1,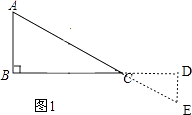 ,
,
当α=180°时,
可得AB∥DE,
∵ ![]() ,
,
∴ ![]() =
= ![]() .
.
故答案为: ![]() .
.
(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出 ![]() 的值是多少.
的值是多少.
②α=180°时,可得AB∥DE,然后根据 ![]() ,求出
,求出 ![]() 的值是多少即可.(2)首先判断出∠ECA=∠DCB,再根据
的值是多少即可.(2)首先判断出∠ECA=∠DCB,再根据 ![]() ,判断出△ECA∽△DCB,即可求出
,判断出△ECA∽△DCB,即可求出 ![]() 的值是多少,进而判断出
的值是多少,进而判断出 ![]() 的大小没有变化即可.(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.
的大小没有变化即可.(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.

【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?