题目内容
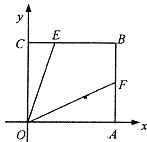
【题目】如图,在正方形OABC中,点B的坐标是(3,3),点E、F分别在边BC、BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
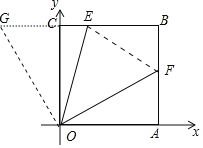
【解析】如图,延长BE到G,使CG=AF,连接OG,EF.由△OAF≌△OCG(SAS),推出∠AOF=∠COG,OF=OG,由△OFE≌△OGE(SAS),推出EF=GE=AF+CE,设AF=x,则EF=1+x,BF=3-x,在Rt△EBF中,根据BE2+BF2=EF2,列出方程即可解决问题.
如图,延长BE到G,使CG=AF,连接OG,EF.
∵四边形OABC为正方形,且点B坐标为(3,3),
∴OA=OC=3;∠A=∠OCG=90°;
在△OAF与△OCG中,
∵OA=OC,∠OAF=∠OCG,AF=CG,
∴△OAF≌△OCG(SAS),
∴∠AOF=∠COG,OF=OG;
∴∠EOG=∠EOC+∠AOF=90°-45°=45°;
在△OFE与△OGE中,
∵OF=OG,∠EOF=∠GOE,OE=OE,
∴△OFE≌△OGE(SAS),
∴EF=GE=AF+CE,设AF=x,则EF=1+x,BF=3-x,
在Rt△EBF中,∵BE2+BF2=EF2,
∴22+(3-x)2=(1+x)2,
∴x=![]() ,
,
∴AF=![]() ,
,
故选D.

练习册系列答案
相关题目