题目内容
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,限用无刻度直尺完成以下作图:
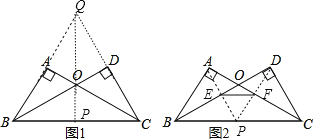
(1)在图1中作线段BC的中点P;
(2)在图2中,在OB、OC上分别取点E、F,使EF∥BC.

【答案】(1)见解析;(2)见解析.
【解析】
(1)延长BA和CD,它们相交于点Q,然后延长QO交BC于P,则PB=PC,根据线段垂直平分线的逆定理可证明;
(2)连结AP交OB于E,连结DP交OC于F,则EF∥BC.分别证明△BEP≌△CFP,△BEP≌△CFP可得∠APB=∠DPC和∠PEF=∠PFE,根据三角形内角和定理和平角的定义可得∠APB=∠PEF,即可证明EF//BC.
解:(1)如图1,点P为所作,
理由如下:∵∠A=∠D=90°,AC=BD,BC=CB,
∴△ABC≌△DCB
∴∠ABC=∠DCB,∠ACB=∠DBC
∴QB=QC,OB=OC
∴Q,O在BC的垂直平分线上,
∴延长QO交BC于P,就有P为线段BC的中点;
(2)如图2,EF为所作.
理由如下:∵△ABC≌△DCB
∴AB=DC,
又∵∠ABC=∠DCB,BP=PC
∴△ABP≌△DCP
∴∠APB=∠DPC
又∵∠DBC=∠ACB,BP=PC
∴△BEP≌△CFP
∴PE=PF
∴∠PEF=∠PFE,
∵∠APB+∠DPC+∠APD=180°
∠PEF+∠PFE+∠APD=180°
∴∠APB=∠PEF
∴EF//BC.

练习册系列答案
相关题目






