题目内容
如图,直线l1:y=kx+b平行于直线y=x-1,且与直线l2:y=mx+| 1 | 2 |
(1)求直线l1、l2的解析式;
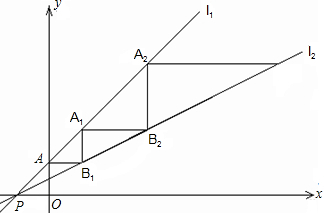
(2)直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
照此规律运动,动点C依次经过点B1,A1,B2,A2,B3,A3,…,Bn,An,…
①求点B1,B2,A1,A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
分析:(1)根据直线l1:y=kx+b平行于直线y=x-1,求得k=1,再由与直线l2:y=mx+
相交于点P(-1,0),分别求出b和m的值.
(2)由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推再求得A1、B2、A2的值,从而得到An、Bn,进而求出点C运动的总路径的长.
| 1 |
| 2 |
(2)由直线l1的解析式,求出A点的坐标,从而求出B1点的坐标,依此类推再求得A1、B2、A2的值,从而得到An、Bn,进而求出点C运动的总路径的长.
解答:解:(1)∵y=kx+b平行于直线y=x-1,
∴y=x+b
∵过P(-1,0),
∴-1+b=0,
∴b=1
∴直线l1的解析式为y=x+1;(1分)
∵点P(-1,0)在直线l2上,
∴-m+
=0;
∴m=
;
∴直线l2的解析式为y=
x+
;(2分)
(2)①A点坐标为(0,1),
则B1点的纵坐标为1,设B1(x1,1),
∴
x1+
=1;
∴x1=1;
∴B1点的坐标为(1,1);(3分)
则A1点的横坐标为1,设A1(1,y1)
∴y1=1+1=2;
∴A1点的坐标为(1,2),即(21-1,21);(4分)
同理,可得B2(3,2),A2(3,4),即(22-1,22);(6分)
②经过归纳得An(2n-1,2n),Bn(2n-1,2n-1);(7分)
当动点C到达An处时,运动的总路径的长为An点的横纵坐标之和再减去1,
即2n-1+2n-1=2n+1-2.(8分)
∴y=x+b
∵过P(-1,0),
∴-1+b=0,
∴b=1
∴直线l1的解析式为y=x+1;(1分)
∵点P(-1,0)在直线l2上,
∴-m+
| 1 |
| 2 |
∴m=
| 1 |
| 2 |
∴直线l2的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)①A点坐标为(0,1),
则B1点的纵坐标为1,设B1(x1,1),
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴x1=1;
∴B1点的坐标为(1,1);(3分)
则A1点的横坐标为1,设A1(1,y1)
∴y1=1+1=2;
∴A1点的坐标为(1,2),即(21-1,21);(4分)
同理,可得B2(3,2),A2(3,4),即(22-1,22);(6分)
②经过归纳得An(2n-1,2n),Bn(2n-1,2n-1);(7分)
当动点C到达An处时,运动的总路径的长为An点的横纵坐标之和再减去1,
即2n-1+2n-1=2n+1-2.(8分)
点评:本题考查了一次函数和几何问题的综合应用,本题中根据点的坐标求出点与点的距离是解题的基础.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
相关题目
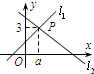 20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为
20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为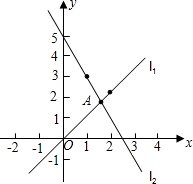 如图,直线l1、l2交于点A,试求点A的坐标.
如图,直线l1、l2交于点A,试求点A的坐标.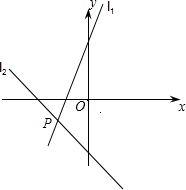 如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是
如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是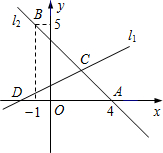 l2交于点C.
l2交于点C.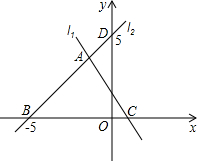 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.