题目内容
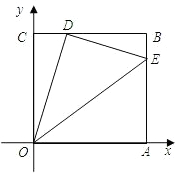
如图边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半 轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t.
轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t.
(1)点D在运动到某一位置时,能否看作是点A关于直线OE对称的对称点,为什么?
(2)用t的代数式表示BE的长?
(3)当t= 时,求直线DE的函数表达式.
时,求直线DE的函数表达式.
解:(1)点D在运动到某一位置时,不能看作是点A关于直线OE对称的对称点.理由如下:
假设点D是点A关于直线OE对称的对称点,那么△ODE≌△OAE,
∴OD=OA=1,
而在直角△OCD中,OC=1,
∴OC=OD,
又∵动点D在线段BC上移动,不与C重合,
∴这与直角三角形中斜边最长相矛盾,
故点D不能看作是点A关于直线OE对称的对称点;
(2)如图,∵四边形OABC是正方形,且DE⊥OD,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3.
又∵∠OCD=∠B=90°,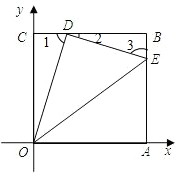
∴△OCD∽△DBE,
∴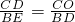 .
.
又∵CD=t,CO=1,BD=BC-CD=1-t,
∴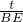 =
= ,
,
∴BE=-t2+t;
(3)当t= 时,BE=-t2+t=
时,BE=-t2+t= ,
,
∴AE=AB-BE=1- =
= ,
,
∴点E的坐标为(1, ).
).
设直线DE的解析式为y=kx+b,
又∵点D的坐标为( ,1),
,1),
∴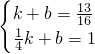 ,
,
解得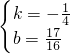
直线DE的解析式为y=- x+
x+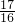 .
.
分析:(1)如果点D看作是点A关于直线OE对称的对称点,那么根据轴对称的性质得出OD=OA=1,而在直角△OCD中,OC=1,与直角三角形中斜边最长相矛盾,故点D不能看作是点A关于直线OE对称的对称点;
(2)根据两角对应相等,两三角形相似,证明出△OCD∽△DBE,由相似三角形的对应边成比例列出比例式,从而可用含t的代数式表示BE的长;
(3)把t= 代入(2),求出BE的长,即可求得点E的坐标为(1,
代入(2),求出BE的长,即可求得点E的坐标为(1, ),又由点D的坐标为(
),又由点D的坐标为( ,1),由待定系数法即可求得直线DE的解析式.
,1),由待定系数法即可求得直线DE的解析式.
点评:本题考查了正方形、轴对称的性质,一次函数的综合应用以及相似三角形的判定与性质等知识点.本题中用相似三角形的性质得出比例关系,然后用线段的比例关系和CD表示出BE是解题的关键.
假设点D是点A关于直线OE对称的对称点,那么△ODE≌△OAE,
∴OD=OA=1,
而在直角△OCD中,OC=1,
∴OC=OD,
又∵动点D在线段BC上移动,不与C重合,
∴这与直角三角形中斜边最长相矛盾,
故点D不能看作是点A关于直线OE对称的对称点;
(2)如图,∵四边形OABC是正方形,且DE⊥OD,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3.
又∵∠OCD=∠B=90°,

∴△OCD∽△DBE,
∴
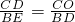 .
.又∵CD=t,CO=1,BD=BC-CD=1-t,
∴
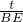 =
= ,
,∴BE=-t2+t;
(3)当t=
 时,BE=-t2+t=
时,BE=-t2+t= ,
,∴AE=AB-BE=1-
 =
= ,
,∴点E的坐标为(1,
 ).
).设直线DE的解析式为y=kx+b,
又∵点D的坐标为(
 ,1),
,1),∴
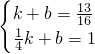 ,
,解得
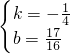
直线DE的解析式为y=-
 x+
x+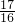 .
.分析:(1)如果点D看作是点A关于直线OE对称的对称点,那么根据轴对称的性质得出OD=OA=1,而在直角△OCD中,OC=1,与直角三角形中斜边最长相矛盾,故点D不能看作是点A关于直线OE对称的对称点;
(2)根据两角对应相等,两三角形相似,证明出△OCD∽△DBE,由相似三角形的对应边成比例列出比例式,从而可用含t的代数式表示BE的长;
(3)把t=
 代入(2),求出BE的长,即可求得点E的坐标为(1,
代入(2),求出BE的长,即可求得点E的坐标为(1, ),又由点D的坐标为(
),又由点D的坐标为( ,1),由待定系数法即可求得直线DE的解析式.
,1),由待定系数法即可求得直线DE的解析式.点评:本题考查了正方形、轴对称的性质,一次函数的综合应用以及相似三角形的判定与性质等知识点.本题中用相似三角形的性质得出比例关系,然后用线段的比例关系和CD表示出BE是解题的关键.

练习册系列答案
相关题目
 轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t.
轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t. 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45° 如图边长为a的正方形ABCD沿直线l向右滚动.当正方形滚动一周时,正方形中心O经过的路程为
如图边长为a的正方形ABCD沿直线l向右滚动.当正方形滚动一周时,正方形中心O经过的路程为 已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )
已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )
