题目内容
 已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )
已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )分析:根据旋转的性质得∠BCF=30°,CB=CF=3,∠F=∠B=90°,则可根据“HL”判断Rt△CHF≌Rt△CHD,所以∠FCH=∠DCH=30°,然后根据含30度的直角三角形三边的关系求解.
解答: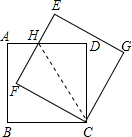 解:连结CH,如图,
解:连结CH,如图,
∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
∴∠BCF=30°,CB=CF=3,∠F=∠B=90°,
∴∠DCF=60°,
而CB=CD=3,
∴CD=CF,
在Rt△CHF和Rt△CHD中
,
∴Rt△CHF≌Rt△CHD,
∴∠FCH=∠DCH,
∴∠DCH=
∠DCF=30°,
∴DH=
DC=
×3=
.
故选A.
 解:连结CH,如图,
解:连结CH,如图,∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
∴∠BCF=30°,CB=CF=3,∠F=∠B=90°,
∴∠DCF=60°,
而CB=CD=3,
∴CD=CF,
在Rt△CHF和Rt△CHD中
|
∴Rt△CHF≌Rt△CHD,
∴∠FCH=∠DCH,
∴∠DCH=
| 1 |
| 2 |
∴DH=
| ||
| 3 |
| ||
| 3 |
| 3 |
故选A.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
相关题目
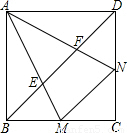
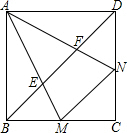 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°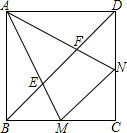 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°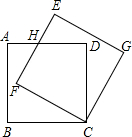 已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为
已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为