题目内容
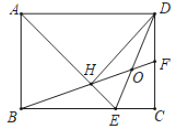
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由四边形ABCD是矩形,∠BAD的平分线交BC于点E,得出AD=BC,∠ABE=∠ADC=90°,∠BAE=∠DAE=45°,则△ABE是等腰直角三角形,得出∠BEH=45°,AE=![]() AB,推出AE=AD=BC,由AAS证得△ABE≌△AHD,故①正确;
AB,推出AE=AD=BC,由AAS证得△ABE≌△AHD,故①正确;
由△ABE≌△AHD,得出∠HDA=45°,AB=BE=DH=AH,则∠HDF=45°,AE-AH=BC-BE,推出∠BEH=∠HDF,HE=CE,故②正确;
由AB=AH,得出∠ABH=∠AHB=∠FHE=![]() (180°-∠BAE)=67.5°,则∠EBH=∠ABE-∠ABH=22.5°,∠DHF=∠DHE-∠FHE=22.5°,推出∠EBH=∠DHF,由ASA证得△EBH≌△DHF,得出BH=HF,即H是BF的中点,故③正确;
(180°-∠BAE)=67.5°,则∠EBH=∠ABE-∠ABH=22.5°,∠DHF=∠DHE-∠FHE=22.5°,推出∠EBH=∠DHF,由ASA证得△EBH≌△DHF,得出BH=HF,即H是BF的中点,故③正确;
由AB=AH,∠BAH=45°,得出△ABH不是等边三角形,则AB≠BH,推出AB≠HF,故④错误.
∵四边形ABCD是矩形,∠BAD的平分线交BC于点E,
∴AD=BC,∠ABE=∠ADC=90°,∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴∠BEH=45°,AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AE=AD=BC,
在△ABE和△AHD中,
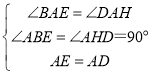 ,
,
∴△ABE≌△AHD(AAS),故①正确;
∵△ABE≌△AHD,
∴∠HDA=45°,AB=BE=DH=AH,
∴∠HDF=45°,AE-AH=BC-BE,
∴∠BEH=∠HDF,HE=CE,故②正确;
∵AB=AH,
∴∠ABH=∠AHB=∠FHE=![]() (180°-∠BAE)=
(180°-∠BAE)=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠EBH=∠ABE-∠ABH=90°-67.5°=22.5°,∠DHF=∠DHE-∠FHE=90°-67.5°=22.5°,
∴∠EBH=∠DHF,
在△EBH和△DHF中,
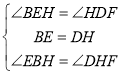 ,
,
∴△EBH≌△DHF(ASA),
∴BH=HF,
∴H是BF的中点,故③正确;
∵AB=AH,∠BAH=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴AB≠HF,故④错误;
综上所述,正确的命题为①②③,
故选:C.