题目内容
【题目】如图1,在平面直角坐标系中,△ABC的顶点A(-3,0)、B(0,3),AD⊥BC交BC于D点,交y轴正半轴于点E(0,t)
(1)当t=1时,求C点的坐标;
(2)如图2,求∠ADO的度数;
(3)如图3,已知点P(0,2),若PQ⊥PC,PQ=PC,求Q的坐标(用含t的式子表示).
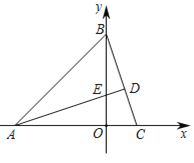
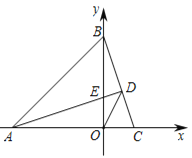
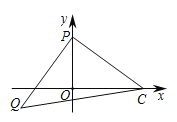
图1 图2 图3
【答案】(1)C(1,0);(2)∠ADO=45°;(3)Q(-2,2-t)
【解析】试题分析: ![]() 根据
根据![]() 得
得![]() ,即可求出点
,即可求出点![]() 坐标.
坐标.
![]() 先过点
先过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,根据
,根据![]() ,得到
,得到![]() ,且
,且![]() ,再根据
,再根据![]() 得出
得出![]() ,进而得到
,进而得到![]() 平分
平分![]() ,求出
,求出![]() 的度数.
的度数.
![]() 过点
过点![]() 作
作![]() 垂直于
垂直于![]() 轴于
轴于![]() ,作
,作![]() 于
于![]() ,如图,易得四边形
,如图,易得四边形![]() 为矩形,证明
为矩形,证明![]() ,则可利用
,则可利用![]() 证明
证明![]() 即可求出点
即可求出点![]() 坐标.
坐标.
试题解析: ![]()
![]() ,
,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
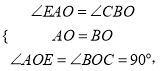
![]()
![]()
∴点![]() 坐标
坐标![]()
![]() 如图,过点
如图,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
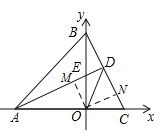
![]()
![]() .
.
![]()
![]()
![]()
![]() 平分
平分![]() .
.
![]()
![]() 过点
过点![]() 作
作![]() 垂直于
垂直于![]() 轴于
轴于![]() ,作
,作![]() 于
于![]() ,
,
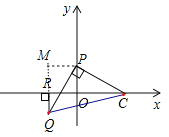
由![]() 知点
知点![]() 的坐标为:
的坐标为: ![]() .
.
四边形![]() 为矩形,
为矩形,
![]()
![]()
在![]() 和
和![]() 中
中
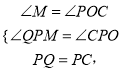
![]()
![]()
![]() 点
点![]() 坐标是
坐标是![]()

练习册系列答案
相关题目