题目内容
【题目】对于二次函数
，有下列说法：
①如果当x≤1时
随
的增大而减小，则m≥1；
②如果它的图象与x轴的两交点的距离是4，则
；
③如果将它的图象向左平移3个单位后的函数的最小值是-4，则m=－1；
④如果当x=1时的函数值与x=2013时的函数值相等，则当x=2014时的函数值为－3．
其中正确的说法是 ．
【答案】①②④．
【解析】
试题分析：①∵当x≤1时y随x的增大而减小，
∴函数的对称轴
在直线x=1的右侧（包括与直线x=1重合），则m≥1，故本选项正确；
②它的图象与x轴的两交点的距离为
，解得
，故②正确；
③将m=﹣1代入解析式，得
，当y=0时，得
，即（x﹣1）（x+3）=0，解得，
，
，将图象向左平移3个单位后不过原点，故本选项错误；
④∵当x=1时的函数值与x=2013时的函数值相等，∴对称轴为
，则
，m=1007，原函数可化为
，当x=2014时，
，故本选项正确．
故答案为：①②④．
练习册系列答案
相关题目
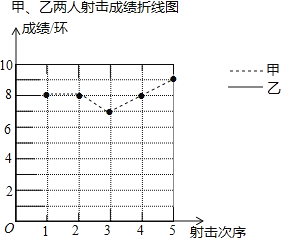
【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为（单位：环）：
甲：8，8，7，8，9
乙：5，9，7，10，9
教练根据他们的成绩绘制了如下尚不完整的统计图表：
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息，请解答下面的问题：
（1）α＝ ，b＝ ，c＝ ；
（2）完成图中表示乙成绩变化情况的折线；
（3）教练根据这5次成绩，决定选择甲参加射击比赛，教练的理由是什么？
（4）若选手乙再射击第6次，命中的成绩是8环，则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 ．（填“变大”、“变小”或“不变”）
