��Ŀ����
����Ŀ�����Ǹ������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ�����������ı���Ϊ�����ı��Σ����������ڵı߳�Ϊ����ı��εĹ��ɱ�.
(1)д������ѧ����������ı������ǹ����ı��ε�����ͼ�ε����� �� ��
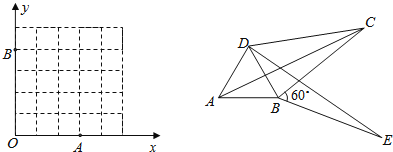
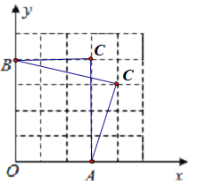
(2)��ͼ1����֪��㣨С�����εĶ��㣩O0,0��A3,0��B0,4����C Ϊͼ�����������е���һ����㣬�ı���OACB ����OA ��OB Ϊ���ɱ��ҶԽ�����ȵĹ����ı��Σ����C �����ꣻ
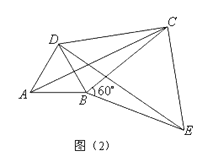
(3)��ͼ2����ABC�� BC AB ���ƶ��� B ��˳ʱ�뷽����ת60���õ�DBE ������ AD ��DC ���ı��� ABCD �ǹ����ı��Σ�����DC ��BC Ϊ���ɱߣ���DCB �Ķ���.
���𰸡���1�����Σ������Σ��𰸲�Ψһ������2��C��3,4������4,3������3����DCB=30��.
��������
��1�����ݾ����������ε����ʿɵô𰸣�
��2�����ù��ɶ����ɵ�AB=5��Ȼ���ڸ����������OC=5�ĵ㼴�ɣ�
��3������CE��������ת�����ʿɵá�ABC�ա�DBE����BC=BE����Ϊ��CBE=60����������BCE�ǵȱ������Σ���BC=CE����BCE=60�������ݹ����ı��εĶ����빴�ɶ������涨���ɵ���DCE=90������ɵ���DCB�Ķ���.
�⣺��1�����Σ������Σ��𰸲�Ψһ����
��2��![]() ��
��
��C��������ͼΪ����3,4������4,3����
��3������CE��
����ת�����ʵã���ABC�ա�DBE����BC=BE��AC=BD��
����CBE=60����
����BCE�ǵȱ������Σ�
��BC=CE����BCE=60����
���ı���ABCDΪ�����ı��Σ�����DC��BCΪ���ɱߣ�
��![]() ��
��
��![]() ��
��
����DCE=90����
���BCD=��DCE����BCE=90����60��=30��.