题目内容
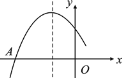
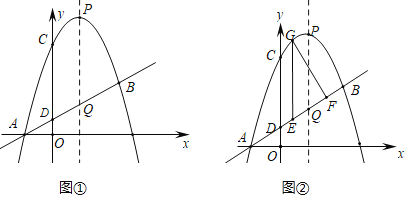
【题目】如图①抛物线y=﹣x2+(m﹣1)x+m与直线y=kx+k交于点A、B,其中A点在x轴上,它们与y轴交点分别为C和D,P为抛物线的顶点,且点P纵坐标为4,抛物线的对称轴交直线于点Q.
(1)试用含k的代数式表示点Q、点B的坐标.
(2)连接PC,若四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点,求k的取值范围.
(3)如图②,四边形CDQP为平行四边形时,
①求k的值;
②E、F为线段DB上的点(含端点),横坐标分别为a,a+n(n为正整数),EG∥y轴交抛物线于点G.问是否存在正整数n,使满足tan∠EGF![]() 的点E有两个?若存在,求出n;若不存在说明理由.
的点E有两个?若存在,求出n;若不存在说明理由.
【答案】(1)Q(1,2k),B(﹣k+3,﹣k2+4k);(2)1<k![]() ;(3)①k=1;②不存在,理由见解析.
;(3)①k=1;②不存在,理由见解析.
【解析】
(1)由图可知,抛物线对称轴在y轴右侧,顶点P纵坐标为4,用顶点坐标公式即列得关于m的不等式和方程,求解即得到m的值,进而得到抛物线解析式.把顶点P的横坐标代入直线y=kx+k即得到用k表示点Q的坐标.令抛物线解析式为0,解方程求得点A坐标.把直线与抛物线解析式联立方程组并整理得关于x的一元二次方程,利用韦达定理得xA+xB的值,把xA代入即求得点B横坐标进而求得B的纵坐标.
(2)由(1)得C(0,3),P(1,4),即四边形CDQP的内部(包括边界和顶点)有2个满足横坐标、纵坐标均为整数的点P、C,另外两个满足的点应该是M(0,2)、N(1,3),由图象可知此时点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合).因为D(0,k),Q(1,2k),即列得关于k的不等式组,求解即得到k的取值范围.
(3)①求直线CP解析式,由四边形CDQP为平行四边形可得DQ∥CP,即直线y=kx+k的k与直线CP解析式的一次项系数相等,求得k=1.
②过点F作FH⊥⊥EG于点H,则Rt△FGH中,tan∠EGF![]() ,即GH=2FH.由点E、F横坐标分别为a,a+n,可用含a、n的式子表示FH、GH的长,代入GH=2FH,得到关于a的一元二次方程(n为常数).因为满足tan∠EGF
,即GH=2FH.由点E、F横坐标分别为a,a+n,可用含a、n的式子表示FH、GH的长,代入GH=2FH,得到关于a的一元二次方程(n为常数).因为满足tan∠EGF![]() 的点E有两个,即关于a的方程有两个不相等的实数根,由△>0求得n的取值范围小于0,故不存在满足条件的正整数n.
的点E有两个,即关于a的方程有两个不相等的实数根,由△>0求得n的取值范围小于0,故不存在满足条件的正整数n.
解:(1)∵抛物线y=﹣x2+(m﹣1)x+m的顶点P纵坐标为4,
∴![]() 4
4
解得:m1=3,m2=﹣5
∵抛物线对称轴在y轴右侧
∴![]() 0
0
解得:m>1
∴m=3
∴抛物线为y=﹣x2+2x+3,顶点P(1,4)
∵直线y=kx+k与对称轴交于点Q
∴Q(1,2k)
∵y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3
∴A(﹣1,0)
∵ 整理得:x2+(k﹣2)x+k﹣3=0
整理得:x2+(k﹣2)x+k﹣3=0
∴xA+xB=﹣(k﹣2)
∴xB=﹣(k﹣2)﹣xA=﹣(k﹣2)﹣(﹣1)=﹣k+3
∴yB=kxB+k=﹣k2+4k
∴B(﹣k+3,﹣k2+4k)
(2)∵C(0,3),P(1,4),D(0,k),Q/span>(1,2k)
∴当四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点时,
4个点是C、P、M(0,2)、N(1,3)(如图1)
∴点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合)
∴![]() ,解得:1<k
,解得:1<k![]()
(3)①∵C(0,3),P(1,4)
∴直线CP解析式为y=x+3
∵四边形CDQP为平行四边形
∴DQ∥CP,即直线y=kx+k平行直线CP
∴k=1
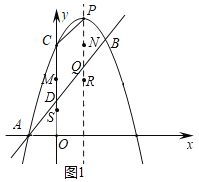
②不存在满足条件的正整数n.
如图2,过点F作FH⊥EG于点H
∴∠FHE=∠FHG=90°
∵k=1
∴直线AB:y=x+1
∵点E在线段DB上横坐标为a,EG∥y轴交抛物线于点G
∴E(a,a+1),G(a,﹣a2+2a+3)
∵点F在线段DB上横坐标为a+n
∴FH=xF﹣xE=n,F(a+n,a+n+1)
∴GH=yG﹣yF=﹣a2+2a+3﹣(a+n+1)=﹣a2+a+2﹣n
∵Rt△FGH中,tan∠EGF![]()
∴GH=2FH
∴﹣a2+a+2﹣n=2n,整理得:a2﹣a+3n﹣2=0
∵满足tan∠EGF![]() 的点E有两个,
的点E有两个,
∴关于a的方程a2﹣a+3n﹣2=0有两个不相等的实数根
∴△=1﹣4(3n﹣2)>0
解得:0<n![]()
∴不存在正整数n,使满足tan∠EGF![]() 的点E有两个.
的点E有两个.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】为了丰富同学们的知识,拓展阅读视野,学习图书馆购买了一些科技、文学、历史等书籍,进行组合搭配成![]() 、
、![]() 、
、![]() 三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
|
|
| |
规格(本/套) | 12 | 9 | 7 |
价格(元/套) | 200 | 150 | 120 |
(1)已知搭配![]() 、
、![]() 两种套型书籍共15套,需购买书籍的花费是2120元,问
两种套型书籍共15套,需购买书籍的花费是2120元,问![]() 、
、![]() 两种套型各多少套?
两种套型各多少套?
(2)若图书馆用来搭配的书籍共有2100本,现将其搭配成![]() 、
、![]() 两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
(3)若图书馆用来搭配的书籍共有122本,现将其搭配成![]() 、
、![]() 、
、![]() 三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.