题目内容
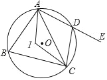
【题目】如图，△ABC的点A，C在⊙O上，⊙O与AB相交于点D，连接CD，∠A＝30°，DC＝
．
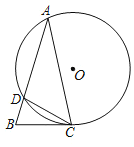
（1）求圆心O到弦DC的距离；
（2）若∠ACB+∠ADC＝180°，求证：BC是⊙O的切线．
【答案】（1）
；（2）详见解析
【解析】
（1）连接OD，OC，过O作OE⊥OC于E，得到△OCD是等边三角形，求得OD=OC=CD=
，解直角三角形即可得到结论；
（2）由（1）得，△ODC是等边三角形，求得∠OCD=60°，根据相似三角形的性质得到∠A=∠BCD=30°，求得∠OCB=90°，于是得到BC是⊙O的切线．
解：（1）连接OD，OC，过O作OE⊥OC于E，
∵∠A＝30°，
∴∠DOC＝60°，
∵OD＝OC，CD＝，
∴△OCD是等边三角形，
∴OD＝OC＝CD＝，
∵OE⊥DC，
∴DE＝
，∠DEO＝90°，∠DOE＝30°，
∴OE＝
DE＝，
∴圆心O到弦DC的距离为：；
（2）由（1）得，△ODC是等边三角形，
∴∠OCD＝60°，
∵∠ACB+∠ADC＝180°，∠CDB+∠ADC＝180°，
∴∠ACB＝∠CDB，
∵∠B＝∠B，
∴△ACB∽△CDB，
∴∠A＝∠BCD＝30°，
∴∠OCB＝90°，
∴BC是⊙O的切线．
练习册系列答案
相关题目
